ЕГЭ Математика (профиль) 2016 Вариант 130

Настенные часы с минутной и часовой стрелкой нельзя заводить, если хотя бы одна из стрелок находится между 3 и 4 или между 8 и 9. Сколько в сутках времени, когда эти часы заводить можно? Ответ дайте в минутах.

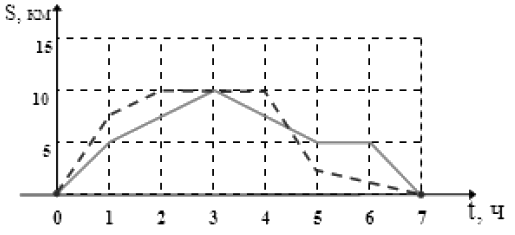
На рисунке приведен график движения двух туристических групп. Определите, на сколько средняя скорость движения туристов на всем протяжении пути одной группы отличается от средней скорости движения туристов на всем протяжении пути другой группы. Ответ дайте в км/ч.

Для приготовления пирожков бабушка из круглого листа теста радиусом 20 см вырезала десять кружков радиусом 5 см. Сколько процентов теста составили остатки, полученные после вырезания кружков?

Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?

Найдите корень уравнения \(sin \frac{\pi x}{2}=x^{2}+6x+10\)

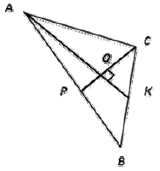
В треугольнике \(ABC\) медианы \(AK\) и \(CP\) пересекаются под прямым углом в точке \(Q\). Найдите длину медианы, проведенной из вершины \(B\) треугольника \(ABC\), если известно, что \(AK=12\), \(CP=9\).

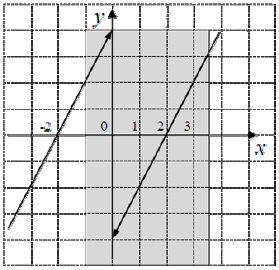
На рисунке изображен график производной функции \(f(x)=x^{2} - 4 \left | x \right | +3\). Найдите наибольшее значение этой функции на отрезке \([-1; 3,5]\).

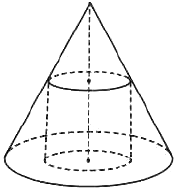
В конус вписан цилиндр так, что плоскость его верхнего основания делит высоту конуса пополам. Найдите объем цилиндра, если объем конуса равен 12.

Найдите значение выражения \(81^{log_{3} \sqrt{2}}-log_{6}9-log_{\frac{1}{\sqrt{6}}} \frac{1}{2}+log_{2}6-log_{2}3\).

Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревателя некоторого прибора задается выражением \(T(t)=T_{0}+at+bt^{2}\), где \(T_{0}=1200 К\), \(a=48 К/мин\), \(b= – 0,4 К/мин^{2}\). Известно, что при температурах нагревателя свыше \(2000 К\) прибор может испортиться, поэтому его нужно отключать. Определите (в минутах), через какое наибольшее время после начала работы нужно отключать прибор.

Пловец потерял под мостом флягу, но заметил это только через 3 мин. Повернув назад, он догнал флягу в 100 м от моста. Найдите скорость течения реки. Ответ дайте в км/ч.

Найдите наименьшее значение выражения \(\sqrt{(x-1)^{2}+(y-5)^{2}}+\sqrt{(x-9)^{2}+(y+10)^{2}}\)

Найдите все корни уравнения \(sin(2^{x})=1\), удовлетворяющие неравенству \(\left | 2^{x}-1 \right | + \left | 2^{x}-8 \right | \leqslant 7 \)

Все плоские углы при вершине \(S\) пирамиды \(SABC\) прямые.
А) Докажите, что точка \(S\), точка пересечения медиан треугольника \(ABC\) и точка, равноудаленная от вершин пирамиды (центр описанной сферы), лежат на одной прямой.
Б) Найдите радиус сферы вписанной в пирамиду \(SABC\), если известно, что \(SA=2, SB=3, SC=4\).

Решите неравенство \(x^{2}+x \sqrt{3-3x^{2}} \geqslant 0,5 + x\)

В равнобокой описанной трапеции \(ABCD\), где угол \(B\) тупой, а \(BC\) и \(AD\) – основания, проведены: 1) биссектриса угла \(B\); 2) высота из вершины \(C)\); 3) прямая, параллельная \(AB)\) и проходящая через середину отрезка \(CD\).
А) Докажите, что все они пересекаются в одной точке.
Б) Найдите расстояние между центрами вписанной и описанной окружностей трапеции \(ABCD\), если известно, что \(BC=8, AD=18\).

Два человека, у которых имеется один велосипед, должны попасть из пункта \(A\) в пункт \(B\), расстояние между которыми 40 км. Первый движется пешком со скоростью 4 км/ч, а на велосипеде – со скоростью 30 км/ч. Второй движется пешком со скоростью 6 км/ч, а на велосипеде – со скоростью 20 км/ч. За какое наименьшее время они могут добраться из \(A\) в \(B\)?
(Велосипед можно оставлять на дороге без присмотра)

Парабола \(p_{2}\) симметрична параболе \(p_{1}\), заданной уравнением \(y=ax^{2} (a>0)\), относительно точки \(T(b; ab^{2}), b>0\). Некоторая прямая пересекает каждую параболу ровно в одной точке: \(p_{1}\) – в точке \(A_{1}\), \(p_{2}\) – в точке \(A_{2}\) так, что угол \(A_{1}A_{2}T\) прямой. Касательная к параболе \(p_1\), проведенная в точке \(T\), пересекает прямую \(A_{1}A_{2}\) в точке \(K\). Найдите отношение, в котором точка \(K\) делит отрезок \(A_{1}A_{2}\).

Решите уравнение:
А) \([2x] = {7x}\);
Б) \([2x] = 7x\);
В) \(2x = {7x}\).

[a] – целая часть числа а, т.е. наибольшее целое число, не превосходящее а; {a} – дробная часть числа а, т.е. {a} = а – [a].