ЕГЭ Математика (профиль) 2016 Вариант 157
Вопрос B1 #3245
Среди 240 000 жителей города Зеленограда 75% не интересуется футболом. Среди футбольных болельщиков 75% планирует 28 мая смотреть по телевизору финал Лиги чемпионов между «Реалом» и «Атлетико». Сколько жителей города Зеленограда планирует смотреть этот матч по телевизору?
Вопрос B2 #3246
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 580 миллиметров ртутного столба?

Вопрос B3 #3247
Окружность с центром в точке О(1; 0) проходит через точку М(-2; 4). Найдите диаметр этой окружности.
Вопрос B4 #3248
Крупье вытаскивает наугад из 36-карточной колоды 3 карты пиковой масти и 1 карту червовой масти и кладет их на стол. Какова вероятность, что пятая вытащенная им карта будет снова червовой масти? (Колода игральных карт содержит по 9 карт каждой из четырех мастей).
Вопрос B5 #3249
Найдите корень уравнения \(\displaystyle 2^{2^{2x+1}}=2\)
Вопрос B6 #3250
В правильном шестиугольнике \(ABCDEF\) \(AD =2 \sqrt{3}\). Найдите \(AE\).
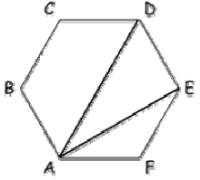
Вопрос B7 #3251
Функция \(y = f (x)\) определена на отрезке [-3; 5]. На рисунке дан график её производной. Найдите количество точек минимума функции \(y = f (x)\).
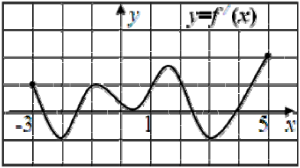
Вопрос B8 #3252
Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
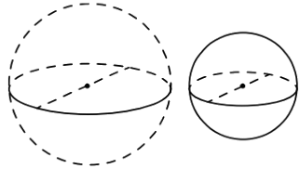
Вопрос B9 #3253
Вычислите: \(\displaystyle 4 cos^{2} \frac{\pi}{8} - 4 cos^{4} \frac{\pi}{8} - 4\)
Вопрос B10 #3254
Девочка массой 60 кг стоит на лыжах. Длина каждой лыжи 1,5 м, ширина 1 дм. Какое давление оказывает девочка на снег? Ответ дайте в кПа. (Считать g=9,8 Н/кг).
Вопрос B11 #3255
Два экскаватора, работая совместно, могут вырыть котлован за 48 ч. Если первый проработает 40 ч, а второй – 30 ч, то будет выполнено 75% всей работы. За какое время может вырыть котлован второй экскаватор, работая отдельно?
Вопрос B12 #3256
Найдите наибольшее значение функции \(\displaystyle f(x)=2- \sqrt[4]{x^{2} - 10x +41}\)
Вопрос B13 #3257
Дано уравнение \(\displaystyle |cos x| = - \sqrt{3} sin x\).
А) Решите уравнение.
Б) Найдите его корни, принадлежащие промежутку \(\left [ 2 \pi ; \frac{7 \pi}{2} \right ] \)
А) Решите уравнение.
Б) Найдите его корни, принадлежащие промежутку \(\left [ 2 \pi ; \frac{7 \pi}{2} \right ] \)
Вопрос B14 #3258
В правильной треугольной призме точка \(P\) – середина ребра \(A_{1}B_{1}\), точка \(M\) – середина ребра \(A_{1}C_{1}\).
А) Докажите, что сечение призмы плоскостью \(BPM\) проходит через точку \(C\).
Б) Найдите отношение объемов многогранников, на которые плоскость \(BPM\) разбивает данную призму, если известно, что \(AB=6\), \(AA_{1}=4\).
А) Докажите, что сечение призмы плоскостью \(BPM\) проходит через точку \(C\).
Б) Найдите отношение объемов многогранников, на которые плоскость \(BPM\) разбивает данную призму, если известно, что \(AB=6\), \(AA_{1}=4\).
Вопрос B15 #3259
Решите неравенство
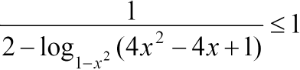
Вопрос B16 #3260
В выпуклом четырехугольнике \(ABCD\) точки \(K, M, P, E\) – середины сторон \(AB\), \(BC\), \(CD\) и \(DA\) соответственно.
А) Докажите, что площадь четырехугольника \(KMPE\) равна половине площади четырехугольника \(ABCD\).
Б) Найдите большую диагональ четырехугольника \(KMPE\), если известно, что \(AC=6, BD=8\), а сумма площадей треугольников \(AKE\) и \(CMP\) равна \(3 \sqrt{3}\).
А) Докажите, что площадь четырехугольника \(KMPE\) равна половине площади четырехугольника \(ABCD\).
Б) Найдите большую диагональ четырехугольника \(KMPE\), если известно, что \(AC=6, BD=8\), а сумма площадей треугольников \(AKE\) и \(CMP\) равна \(3 \sqrt{3}\).
Вопрос B17 #3261
В начале года фирма «Жилстройсервис» выбирает банк для получения кредита среди нескольких банков, кредитующих под разные проценты. Полученным кредитом фирма планирует распорядиться следующим образом: 75% кредита направить на строительство коттеджей, а остальные 25% на оказание риэлтерских услуг населению. Первый проект может принести прибыль в размере от 36% до 44% годовых, а второй - от 20% до 24% годовых. В конце года фирма должна вернуть кредит банку с процентами и при этом рассчитывает на чистую прибыль от указанных видов деятеьности от не менее 13%, но и не более 21% годовых от всего полученного кредита. Какими должны быть наименьшая и наибольшая процентные ставки кредитования выбираемых банков, чтобы фирма гарантированно обеспечила себе указанный выше уровень прибыли?
Вопрос B18 #3262
Для каждого допустимого значения а решите неравенство
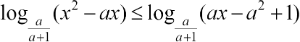
Вопрос B19 #3263
А) Существует ли натуральное число, которое при делении на 2015 дает в остатке 2014, а при делении на 2016 дает в остатке 2015?
Б) Существует ли натуральное число, которое при делении на 3 дает в остатке 2, при делении на 5 дает в остатке 4, а при делении на 10 дает в остатке 6?
В) Найдите наименьшее натуральное число, которое при делении на 2 дает в остатке 1, при делении на 3 дает в остатке 2, …, при делении на 9 дает в остатке 8, при делении на 10 дает в остатке 9.