ЕГЭ Математика (профиль) 2016 Вариант 133
Вопрос B1 #2588
В школе в 9-х классах учится 133 учащихся. Согласно статистике 40% выпускников 9-х классов уходят из школы. На ЕГЭ математику профильного уровня выбирают 60% 11-классников. Из сдающих математику профильного уровня лишь 2% сдают на 80 баллов и более. Сколько учеников нынешних 9-х классов в этой школе согласно статистике сдадут ЕГЭ по математике не менее чем на 80 баллов? Ответ округлите до целого числа.
Вопрос B2 #2589
На диаграмме показано количество посетителей сайта (с округлением до 10000) во все дни с 10 по 29 октября 2015 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Определите по диаграмме, сколько дней количество посетителей сайта было не менее 133000.

Вопрос B3 #2590
Пусть \(\vec{a}=\overline{AB},\vec{c}=\overline{CD}\). Найдите длину вектора \(\vec{a}-\vec{b}\), если \(A(133;-516), B(-568;-656), C(-146;118), D(-982;330)\).
Вопрос B4 #2591
В торговом центре два разных автомата продают кофе. Вероятность того, к концу дня закончится кофе в первом автомате, равна 0,32, что закончится кофе во втором автомате - 0,24. Вероятность того, что закончится кофе в обоих автоматах, равна 0,133. Найдите вероятность того, что к концу дня кофе останется кофе в обоих автоматах.
Вопрос B5 #2592
Найдите корень уравнения \(log_{133} \left( x^{2}-5x \right)=2log_{133}(7x-57)\). Если уравнение имеет более одного корня, в ответе укажите больший из них.
Вопрос B6 #2593
Гипотенуза равнобедренного прямоугольного треугольника равна \(133(\sqrt{2}+1)\). Найдите радиус вписанной в треугольник окружности.
Вопрос B7 #2594
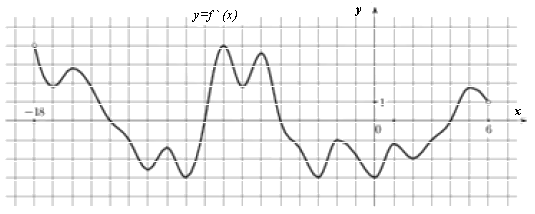
На рисунке изображён график \(y={f}'(x)\) – производной функции \(f(x)\), определённой на интервале \((-18;6)\). Найдите количество точек функции на интервале \((-12;2]\), в которых касательная к графику функции параллельна прямой \(y=133-2x\).
Вопрос B8 #2595
В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 12. Объём цилиндра, описанного около этой пирамиды, равен \(13351 \pi\) . Найдите высоту призмы.
Вопрос B9 #2596
Найдите значение выражения \(\frac{133 - 266 sin^{2}19^{\circ}}{4 - 8 cos^{2}19^{\circ}}\).
Вопрос B10 #2597
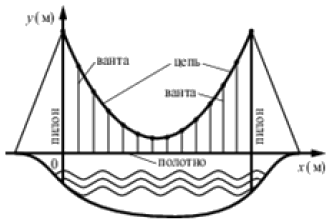
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: Ось \(Oy\) направим вертикально вдоль одного из пилонов, а ось \(Ox\) направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой \(y=0,005x^{2} - 0,74x + 25\), где \(x\) и \(y\) измеряются в метрах. Длина одной из вант, расположенной в левой половине моста, равна \(13,3 м\). Найдите, на каком расстоянии от левого пилона находится эта ванта. Ответ дайте в метрах.
Вопрос B11 #2598
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 18250 рублей, через три года был продан за 13304,25 рублей.
Вопрос B12 #2599
Найдите наименьшее значение функции \(y=x^{7} - 12,75x^{4} - 40x + 133\) на отрезке [-1;3].
Вопрос B13 #2600
Дано уравнение \(sin (133\pi - 21x) \cdot sin \left( 14x+ \frac{133 \pi}{2} \right )=1\)
а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие промежутку \(\left [-\frac{\pi}{2};\frac{3 \pi}{8} \right )\).
а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие промежутку \(\left [-\frac{\pi}{2};\frac{3 \pi}{8} \right )\).
Вопрос B14 #2601
Все стороны правильной шестиугольной призмы \(ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}\) равны
\(\sqrt{133}\).
а) Построить сечение пирамиды плоскостью \(AFC_{1}\).
б) Найдите площадь этого сечения.
а) Построить сечение пирамиды плоскостью \(AFC_{1}\).
б) Найдите площадь этого сечения.
Вопрос B15 #2602
Решите неравенство \(log_{2} \left ( log_{3} \left ( log_{4} \left ( log_{5}^{2} (133-2x) +7 \right ) + 25 \right ) - 1 \right ) \leqslant 1\)
Вопрос B16 #2603
Внутри равностороннего треугольника \(ABC\) в произвольном месте поставлена точка \(M\).
а) Докажите, что сумма расстояний от точки \(M\) до сторон треугольника \(ABC\) равна высоте этого треугольника.
б) Найдите расстояние от точки \(M\) до стороны \(AB\), если расстояние от точки \(M\) до сторон \(AC\) и \(BC\) соответственно равны \(10 \sqrt{133}\) и \(3 \sqrt{133}\), а площадь треугольника \(ABC\) равна \(14364 \sqrt{3}\).
а) Докажите, что сумма расстояний от точки \(M\) до сторон треугольника \(ABC\) равна высоте этого треугольника.
б) Найдите расстояние от точки \(M\) до стороны \(AB\), если расстояние от точки \(M\) до сторон \(AC\) и \(BC\) соответственно равны \(10 \sqrt{133}\) и \(3 \sqrt{133}\), а площадь треугольника \(ABC\) равна \(14364 \sqrt{3}\).
Вопрос B17 #2604
Василий кладёт в банк 1000000 рублей под 10% годовых на 4 года (проценты начисляются один раз после истечения года) с правом докладывать три раза (в конце каждого года) на счёт фиксированную сумму 133000 рублей. Какая сумма будет на счёте у Василия через 4 года?
Вопрос B18 #2605
Найдите все значения \(a\), при каждом из которых наибольшее значение функции
\(f(x)=133ax- \left | x^{2} - 10x +24 \right | \)
больше \(-2\) .
\(f(x)=133ax- \left | x^{2} - 10x +24 \right | \)
больше \(-2\) .
Вопрос B19 #2606
а) Известно, что \(35!=10333147966386144929*66651337523200000000\). Найдите цифру, заменённую звездочкой.
б) Делится ли число \(11^{n+2}+12^{2n+1}\) на \(133\) при любом натуральном \(n\)?
в) Найдите количество натуральных чисел, меньших \(133\), взаимно простых с числом \(133\).
б) Делится ли число \(11^{n+2}+12^{2n+1}\) на \(133\) при любом натуральном \(n\)?
в) Найдите количество натуральных чисел, меньших \(133\), взаимно простых с числом \(133\).