ЕГЭ Математика (профиль) 2016 Вариант 129
Вопрос B1 #2312
Витя в булочной должен купить батон за 26 руб., ржаной хлеб за 19 руб. и три плюшки по цене 14 руб. за штуку. Сколько рублей сдачи получит Витя, если рассчитается за покупку 100-рублевой купюрой?
Вопрос B2 #2313
На графике приведена зависимость высоты \(h\) (в метрах), брошенного вверх тела, от времени \(t\) (в секундах). Определите, сколько секунд тело находилось на высоте не менее 6 метров.

Вопрос B3 #2314
На рисунке клетка имеет размер 1см х 1см. Найдите длину отрезка \(PK\). Ответ дайте в сантиметрах.

Вопрос B4 #2315
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна \(0,4\), а при каждом последующем – \(0,6\). Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее \(0,95\)?
Вопрос B5 #2316
Найдите корень уравнения \(\sqrt{x}=-2x\).
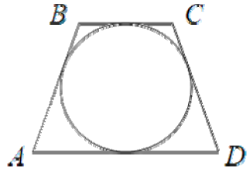
Вопрос B6 #2317
В равнобедренную трапецию \(ABCD\) вписана окружность. Найдите длину боковой стороны \(AB\), если \(BC=3,5, AD=6\).
Вопрос B7 #2318
Функция \(y = f (x)\) определена на промежутке \([-4; 4]\). На рисунке приведен график её производной. Найдите количество точек графика функции \(y = f (x)\), касательная в которых образует с положительным направлением оси \(Ox\) угол \(50 ^{\circ}\).

Вопрос B8 #2319
Площадь боковой поверхности конуса равна 24. Через середину его высоты параллельно основанию провели плоскость. Найдите площадь боковой поверхности усеченного конуса.

Вопрос B9 #2320
Найдите значение выражения \( \frac{log_{5}27}{log_{5}4 - log_{5}36}\).
Вопрос B10 #2321
При адиабатическом процессе для идеального газа выполняется закон \(pV^{k} =const\), где \(p\) – давление газа в паскалях, \(V\) – объём газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него \(k= \frac{5}{3}\) ) из начального состояния, в котором \(const = 10^{5} Па \cdot м^{5}\), газ начинают сжимать. Какой наибольший объём \(V\) может занимать газ при давлениях \(p\) не ниже \(3,2 \cdot 10^{6} Па\)? Ответ выразите в кубических метрах.
Вопрос B11 #2322
Из пункта F круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 15 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Вопрос B12 #2323
Найдите точку минимума функции \(f(x)=(x^{2}-7x+10) \cdot e^{0,5x}\).
Вопрос B13 #2324
Дано уравнение \( \sqrt{tg x} \cdot (2sin^{2}x-sin x-1)=0\)
А) Решите уравнение.
Б) Укажите его корни из промежутка \( \left [ \frac{\pi}{2}; 2 \pi \right ] \).
А) Решите уравнение.
Б) Укажите его корни из промежутка \( \left [ \frac{\pi}{2}; 2 \pi \right ] \).
Вопрос B14 #2325
Дана правильная треугольная призма \(ABCA_{1}B_{1}C_{1}\).
А) Докажите, что объем пирамиды с вершинами в точках \(A, B_{1}, B, C_{1}\) составляет третью часть объема призмы.
Б) Найдите угол между прямыми \(AB_{1}\) и \(BC_{1}\), если известно, что \(AB=2, AA_{1}=4\).
А) Докажите, что объем пирамиды с вершинами в точках \(A, B_{1}, B, C_{1}\) составляет третью часть объема призмы.
Б) Найдите угол между прямыми \(AB_{1}\) и \(BC_{1}\), если известно, что \(AB=2, AA_{1}=4\).
Вопрос B15 #2326
Решите неравенство \(log_{x+1}2 \leqslant log_{3-x}2\)
Вопрос B16 #2327
В равнобедренную трапецию \(ABCD\) с основаниями \(BC\) и \(AD\) вписана окружность. Вторая окружность, построенная на боковой стороне \(AB\) как на диаметре, второй раз пересекает большее основания \(AD\) в точке \(H\).
А) Докажите, что треугольник \(CHD\) равнобедренный.
Б) Найдите основания трапеции, если радиусы первой и второй окружностей равны соответственно \(6\) и \(6,5\).
А) Докажите, что треугольник \(CHD\) равнобедренный.
Б) Найдите основания трапеции, если радиусы первой и второй окружностей равны соответственно \(6\) и \(6,5\).
Вопрос B17 #2328
На первом складе находятся коробки с простыми карандашами, а на втором – с цветными. Количество коробок простых карандашей составляет \(\frac{14}{17}\) от числа коробок цветных карандашей. Когда со складов продали \(\frac{3}{8}\) коробок простых карандашей и \(\frac{5}{9}\) цветных, то на первом складе осталось менее 3000 коробок, а на втором – не менее 2000 коробок. Сколько коробок было первоначально на каждом складе?
Вопрос B18 #2329
Найдите все положительные значения \(a\), при каждом из которых любой корень уравнения \((0,5)^{x}-3x-\sqrt[3]{x}+4=a(5-log_{3}(1-2x))\) находится в промежутке \([-1;0]\)
Вопрос B19 #2330
А) Сколько решений в неотрицательных целых числах имеет уравнение \(a+b=99\)?
Б) Сколько решений в неотрицательных целых числах имеет система уравнений \(\begin{cases} & a+b=99 \\ & c+d=99\end{cases}\)
В) Сколько решений в неотрицательных целых числах имеет уравнение \(a+b+c=99\)?
Б) Сколько решений в неотрицательных целых числах имеет система уравнений \(\begin{cases} & a+b=99 \\ & c+d=99\end{cases}\)
В) Сколько решений в неотрицательных целых числах имеет уравнение \(a+b+c=99\)?