ЕГЭ Математика (профиль) 2016 Вариант 126

Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Нужно приготовить 12 пол-литровых банок маринада. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек лимонной кислоты нужно купить хозяйке?

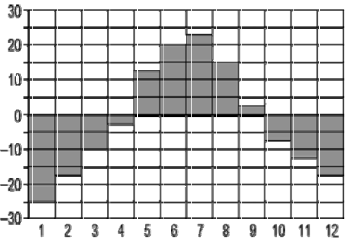
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге за каждый месяц 1972 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, какой была средняя температура в самом холодном зимнем месяце.

Площадь круга, изображенного на клетчатой бумаге, равна 48. Найдите площадь не закрашенного сектора.

В турнире чемпионов участвуют 6 футбольных клубов: «Барселона», «Ювентус», «Бавария», «Челси», «Порту» и «ПСЖ». Команды случайным образом распределяют на две группы по три команды. Какова вероятность того, что «Барселона» и «Бавария» окажутся в одной группе?

Найдите корень уравнения \( \left ( 0,5 \right ) ^{x+2}=16\).

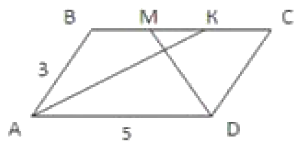
В параллелограмме \(ABCD\) \(AK\) – биссектриса угла \(A\), \(DM\) – биссектриса угла \(D\). Найдите длину отрезка \(KM\), если известны стороны параллелограмма \(AB=3\), \(AD=5\).

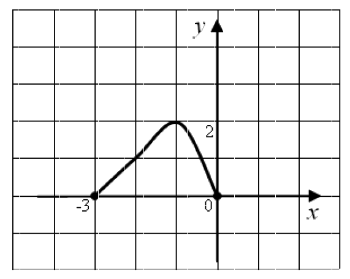
Известно, что \(f (x)\) – нечётная периодическая функция с наименьшим положительным периодом, равным \(6\). На рисунке изображен ее график на отрезке \([-3; 0]\). Вычислите \(7 f(8) – 8 f(-7)\).

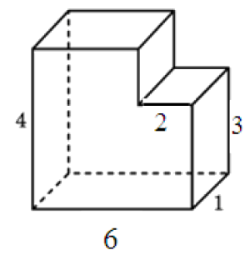
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Найдите значение выражения \(\frac{sin26^{\circ}-sin86^{\circ}}{2sin34^{\circ}}\).

При температуре \(0 ^{\circ}C\) рельс имеет длину \(l_{0}=12,5\) м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону \(l(t^{\circ})=l_{0}(1+ \alpha t^{\circ} )\), где \(\alpha=1,2 \cdot 10^{-5}\) \((C^{\circ})^{-1}\) коэффициент теплового расширения, \(t^{\circ}\) – температура (в градусах Цельсия). При какой температуре рельс удлинится на \(6\) мм? Ответ выразите в градусах Цельсия.

Имеется два сосуда. Первый содержит 30 кг, а второй -20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится во втором сосуде?

Найдите точку максимума функции \(y=x^{2} \cdot e^{x}\).

Дано уравнение \(5 \cdot \left( \frac{1}{5} \right )^{cos 2x}=5^{sin 2x} \)
a) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие интервалу \(\left (-\frac{7\pi}{2} ; -2\pi \right ) \).

В прямоугольном параллелепипеде \(ABCDA_{1}B_{1}C_{1}D_{1}\) \(AB=8\), \(BC=6\), \(AA_{1}=12\). Точка \(К\) – середина ребра \(AD\), точка \(M\) лежит на ребре \(DD_{1}\) так, что \(DM:D_{1}M=1:2\).
а) Докажите, что прямая \(BD_{1}\) параллельна плоскости \(CKM\).
б) Найдите площадь сечения параллелепипеда плоскостью \(CKM\) .

Решите неравенство \(log_{(x-2)^{2}}\frac{5-x}{4-x} \leqslant 1+ log_{(x-2)^{2}} \frac{1}{x^{2}-9x+20} \)

Точка \(M\) лежит на диаметре \(AB\) окружности с центром \(O\). \(C\) и \(D\) – точки окружности, расположенные по одну сторону от \(AB\), причем \(\angle CMA = \angle DMB\).
а) Докажите, что \(\angle OCM = \angle ODM \).
б) Найдите площадь четырехугольника \(COMD\), если известно, что \(OM = 4\), \(BM = 2\), \(\angle CMA=\angle DMB= 45^{\circ}\) .

Города А и В расположены на берегу реки, причем город В лежит ниже по течению. В 6 часов утра из А в В отправился плот. В тот же момент из В в А отправилась лодка, которая встретилась с плотом в 11 часов утра. Доплыв до города А, лодка сразу же повернула обратно и приплыла в город В одновременно с плотом. Успели ли лодка и плот прибыть в город В к 6 ч вечера того же дня?

Найдите все \(a\), при каждом из которых функция \(f (x) = x^{3} - 3ax^{2} + 3a^{2}x - 3 \left | x \right | +3\) имеет ровно два экстремума на промежутке \((-2; 3)\).

а) Может ли сумма четырех натуральных чисел равняться произведению этих же четырех чисел?
б) Может ли сумма четырех различных натуральных чисел равняться произведению этих же четырех чисел?
в) Может ли сумма 2015 различных положительных рациональных чисел равняться произведению этих же 2015 чисел?