ЕГЭ Математика (профиль) 2013 Вариант 7

Диагональ экрана телевизора равна 24 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

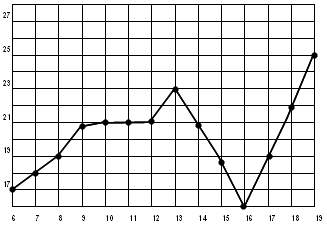
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.

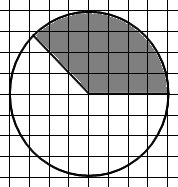
На клетчатой бумаге нарисован круг, площадь которого равна 56. Найдите площадь заштрихованной фигуры.

Телефонная компания предоставляет на выбор три тарифных плана.

Тарифный план	Абонентская плата	Плата за 1 минуту  разговора
Повременный	Нет	0,25 руб.
Комбинированный	140 руб. за 320 мин в месяц	0,2 руб. за 1 мин сверх 320 мин в месяц
Безлимитный	150 руб. в месяц

Абонент выбрал наиболее дешёвый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 700 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 700 минут? Ответ дайте в рублях.

Найдите корень уравнения \(3^{2-x}=81\)

В треугольнике \(ABC\) \(AC = BC = 4\), \(sin B = \frac{\sqrt{19}}{10}\). Найдите \(AB\).

Найдите значение выражения \(log_{14}294 - log_{14} 1,5\)

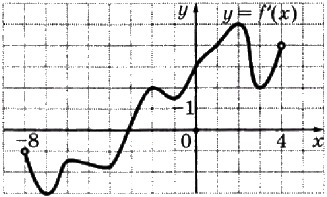
На рисунке изображён график производной функции \(f(x)\), определённой на интервале (-8; 4). Найдите точку экстремума функции \(f(x)\) на отрезке \([-7; 0]\)

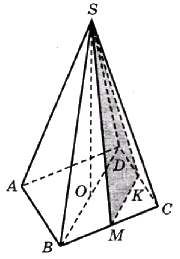
В правильной четырёхугольной пирамиде \(SABCD\) высота \(SO\) равна 9, диагональ основания \(BD\) равна 8. Точки \(K\) и \(M\) — середины рёбер \(CD\) и \(BC\) соответственно. Найдите тангенс угла между плоскостью \(SMK\) и плоскостью основания \(ABC\).

Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Меркурий» по очереди играет с командами «Марс», «Юпитер» и «Уран». Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда «Меркурий».

Кубик весит 800 г. Сколько граммов будет весить кубик, ребро которого в 2 раза меньше, чем ребро первого кубика, если оба кубика изготовлены из одинакового материала?

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \(F_{A}=\alpha\rho gr^{3}\), где \(\alpha =4,2\) — постоянная, \(r\) — радиус аппарата в метрах, \(\rho = 1000 кг/м^{3}\) — плотность воды, a \(g\) — ускорение свободного падения (считайте \(g\) = 10 H/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 5250000 Н? Ответ выразите в метрах.

На изготовление 20 деталей первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 60 таких же деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час делает второй рабочий?

Найдите наибольшее значение функции

\(y= 4 tg x — 4x + \pi - 7\)

на отрезке \(\left [ -\frac{\pi}{4};\frac{\pi}{4} \right ]\)