ЕГЭ Математика (профиль) 2016 Вариант 125

При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?

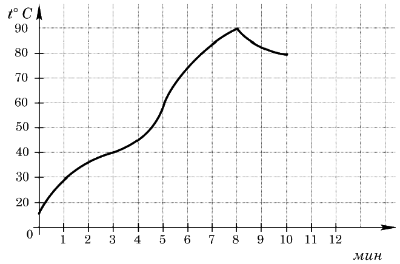
На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры \(60^{\circ}C\) до температуры \(90^{\circ}C\).

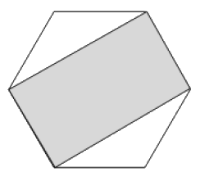
Площадь правильного шестиугольника равна 72. Найдите площадь закрашенного четырехугольника.

Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

Найдите корень уравнения \(\frac{x+11}{x-12}=\frac{x+11}{x-13}\).

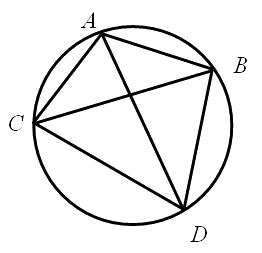
Четырехугольник \(ABCD\) вписан в окружность. Известно, что \(\angle CAD=52^{\circ}, \angle BCD=63^{\circ}\). Найдите \(\angle CDB\). Ответ дайте в градусах.

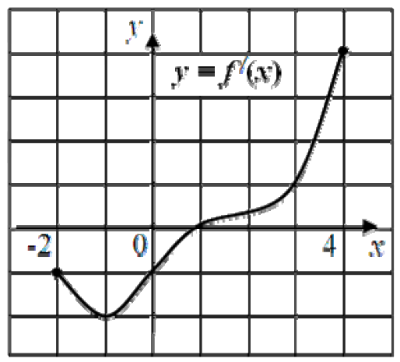
Функция \(y = f (x)\) определена на отрезке \([-2; 4]\). На рисунке дан график её производной. Найдите абсциссу точки графика функции \(y = f (x)\), в которой она принимает наименьшее значение.

Объем фужера, имеющего форму конуса, равен 240 мл. В фужер налили лимонад, при этом уровень жидкости составил \(\frac{1}{4}\) высоты. Сколько миллилитров лимонада нужно долить в фужер, чтобы он оказался полон?

Найдите значение выражения \(\frac{\sqrt{2}-\sqrt{72}}{\sqrt{32}}\)

По закону Ома для полной цепи сила тока, измеряемая в амперах, равна \(I=\frac{\varepsilon }{R+r} \), где \(\varepsilon\) – ЭДС источника (в вольтах), \(r=2,5 Om\) – его внутреннее сопротивление, \(R\) – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более \(25%\) от силы тока короткого замыкания \(I_{к.з.}=\frac{\varepsilon}{r}\)? (Ответ выразите в омах).

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Найдите наименьшее значение функции \(f(x)=\frac{x^{2}+16}{x}\) на отрезке \([2;5]\)

Дано уравнение \(\sqrt{sin x + 3}=-2 sin x\)
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку \([0;2 \pi]\)

В правильной треугольной пирамиде \(PABC\) боковое ребро равно \(10\), а сторона основания равна \(2\sqrt{30}\) . Через точки \(B\) и \(C\) перпендикулярно ребру \(PA\) проведена плоскость \(\alpha\).
а) Докажите, что плоскость \(\alpha\) делит пирамиду \(PABC\) на два многогранника, объемы которых относятся как \(2:3\).
б) Найдите площадь сечения пирамиды \(PABC\) плоскостью \(\alpha\).

Решите неравенство \(\frac{2\sqrt{x+3}}{x+1} \leqslant \frac {3\sqrt{x+3}}{x+2}\)