ЕГЭ Математика (профиль) 2015 Вариант 110
Вопрос B1 #1641
В доме, в котором живёт Петя, 9 этажей и несколько подъездов. Во всех подъездах на каждом этаже находится по 4 квартиры. Петя живёт в квартире № 228. Определите этаж, на котором живёт Петя
Вопрос B2 #1642
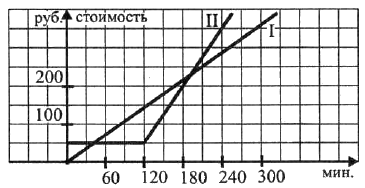
Компания предлагает на выбор два разных тарифа для оплаты телефонных разговоров. Для каждого из этих тарифов изображён график зависимости стоимости разговоров от их общей длительности. Какова максимальная сумма (в рублях), которую придётся заплатить за 210 минут разговора при использовании какого-либо из двух указанных тарифов?
Вопрос B3 #1643
Строительной фирме нужно приобрести 12500 кирпичей у одного из трёх поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей придётся заплатить за самую дешёвую покупку с учётом доставки?
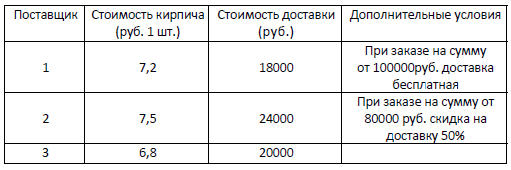
Вопрос B4 #1644
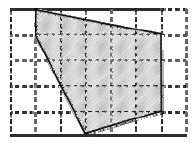
Найдите площадь закрашенной фигуры в квадратных сантиметрах, если размер клетки 1 см х 1 см.
Вопрос B5 #1645
Некоторый прибор состоит из трёх блоков. Если в работе одного из блоков происходит сбой, прибор отключается. Вероятность сбоя в течении года для первого блока составляет 0,2, для второго блока – 0,3, а для третьего блока – 0,1. Какова вероятность, что в течение года произойдёт хотя бы одно отключение данного прибора?
Вопрос B6 #1646
Найдите корень уравнения \(\sqrt{\frac{2x-54}{-x}}=4\).
Вопрос B7 #1647
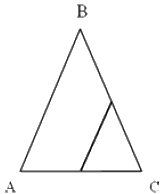
В равнобедренном треугольнике \(ABC\) основание \(AC=4\), \(sin A=\frac{2 \sqrt{2}}{3}\). Найдите отрезок, соединяющий середины сторон \(AC\) и \(BC\).
Вопрос B8 #1648
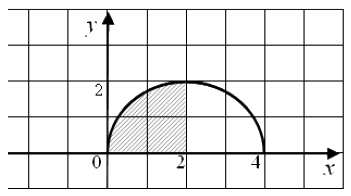
Используя геометрический смысл определенного интеграла, вычислите \(\frac{1}{\pi }\int_{0}^{2} \sqrt{4x-x^{2}}dx\).
Вопрос B9 #1649
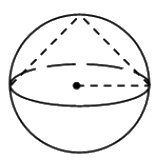
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите объем шара, если объем конуса равен 12.
Вопрос B10 #1650
Вычислите \(\sqrt{8} \cdot cos^{2} \frac{3 \pi}{8} - \sqrt{2}\).
Вопрос B11 #1651
Перед отправкой тепловоз издал гудок с частотой \(f_{0} = 490\) Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из‐за эффекта Доплера частота второго гудка \(f\) больше первого: она зависит от скорости тепловоза по закону \(f(v)=\frac{f_{0}}{1-\frac{v}{c}}\) (Гц), где \(c\) – скорость звука в воздухе (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы. Считать \(с\) = 340 м/с. Ответ выразите в м/с.
Вопрос B12 #1652
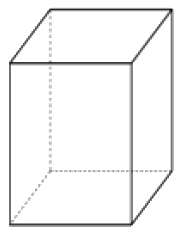
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 9. Площадь полной поверхности этого параллелепипеда равна 484. Найдите третье ребро, выходящее из той же вершины.
Вопрос B13 #1653
Моторная лодка проплыла против течения реки 96 км и вернулась в пункт отправления, затратив на обратный путь на 10 часов меньше, чем на путь против течения. Найдите скорость течения реки, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
Вопрос B14 #1654
Найдите наименьшее значение функции \(f(x)=x^{3}(3x+4)-12(x^{2}+1)\) на отрезке \([-1;2]\).