ЕГЭ Математика (профиль) 2015 Вариант 98

Больному прописаны инъекции лекарства, которые нужно делать по ампуле 0,6 г три раза в день в течение 28 дней. В одной упаковке 10 ампул лекарства по 0,6 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

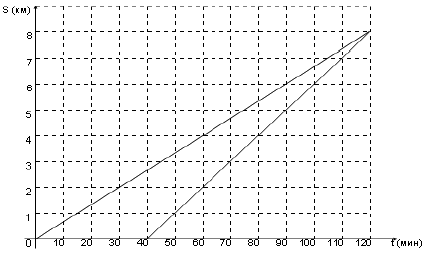
Из пункта Б в пункт А вышел Витя, а через 40 минут после этого из Б в А вышел Миша. Оба мальчика двигались с постоянными скоростями и прибыли в пункт А одновременно. На рисунке приведены графики движения Вити и Миши. По оси абсцисс откладывается время в минутах, а по оси ординат – расстояние в километрах. Определите по графику, на каком расстоянии от пункта А будет находиться Миша через час после выхода Вити из пункта Б. Ответ дайте в километрах.

Своему клиенту компания сотовой связи решила предоставить на выбор одну из скидок. Либо скидку 30% на звонки абонентам других сотовых компаний в своем регионе, либо скидку 15% на звонки абонентам стационарных телефонов, либо 25% на услуги мобильного интернета.

Клиент посмотрел распечатку своих звонков и выяснил, что за месяц он потратил 200 рублей на звонки абонентам других компаний в своем регионе, 300 рублей на звонки абонентам стационарных телефонов и 260 рублей на мобильней интернет. Клиент предполагает, что в следующем месяце затраты будут такими же, и, исходя из этого, выбирает наиболее выгодную для себя скидку. Какую скидку выгоднее выбрать? В ответе запишите, сколько рублей составит эта скидка

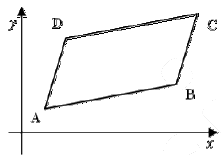
На координатной плоскости задан параллелограмм \(ABCD\). Известно, что \(A(1; 1), B(7; 2), D(2; 4)\). Найдите ординату точки \(C\).

На складе лежат 200 фонариков (без ламп), из них 10 бракованные, а также 500 ламп для фонариков, из них 30 бракованные. Эксперт наугад выбирает один фонарик и одну лампу, ввинчивает ее в фонарик. Найдите вероятность того, что лампа будет гореть (для этого лампа и фонарик должны быть без брака).

Найдите корень уравнения \(log_{\frac{1}{16}}(16-x)=-2\).

На клетчатой бумаге изображен угол \(ACB\). Найдите косинус угла \(ACB\).

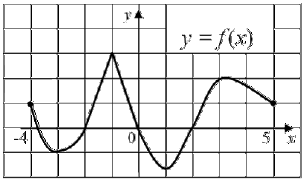
На рисунке приведен график функции \(y=f(x)\), определенной на отрезке \([-4; 5]\). Найдите количество точек графика функции \(y = f (x)\), касательная в которых параллельна прямой \(y = x-5\) или совпадает с ней.

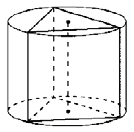
В цилиндр вписана правильная треугольная призма. Найдите объем призмы, если радиус основания цилиндра равен \(\sqrt{2}\) , а его образующая равна \(\sqrt{3}\) .

Найдите значение выражения \(\frac{\left ( 2^{\frac{4}{7}} \cdot 9^{\frac{2}{3}}\right )^{21}}{18^{12}}\).

Операционная прибыль предприятия за краткосрочный период вычисляется по формуле \(\pi (q) = q \cdot ( p - v) - f \). Компания продает свою продукцию по цене \(p = 400 руб.\) за штуку, затраты на производство одной единицы продукции составляют \(v = 300 руб.\) за штуку, постоянные расходы предприятия \(f = 800 000 руб.\) в месяц. Определите наименьший месячный объем производства \(q\) (шт.), при котором прибыль предприятия будет не меньше \(700 000 руб.\) в месяц.

В правильной шестиугольной пирамиде сторона основания равна \(4\sqrt{3}\) , а высота равна \(8\). Найдите длину апофемы данной пирамиды.

Два магазина получили на продажу одинаковые партии мороженого. Известно, что второй магазин установил цену на мороженое на 15% выше, чем первый, но смог продать лишь 95% от всей партии. Первый же магазин реализовал все мороженое. Определите, какой магазин получил большую выручку от продажи мороженого. В ответе укажите, на сколько %.

Найдите наибольшее значение функции \(f(x)=cos 2x+sin x\).