ЕГЭ Математика (профиль) 2013 Вариант 9

Хозяин овощной лавки купил на оптовом рынке 100 кг помидоров и заплатил 4000 рублей. После продажи помидоров оказалось, что за время хранения в лавке 10% помидоров испортились, и хозяин не смог их продать. Остальные помидоры он продал по цене 50 руб. за килограмм. Какую прибыль он получил?

На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по математике в 2007 году (по 1000-балльной шкале). Среди указанных стран второе место принадлежит США. Определите, какое место занимает Швеция.

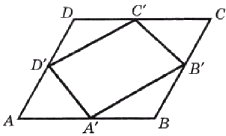
Площадь параллелограмма \(ABCD\) равна 6. Найдите площадь параллелограмма \(A'B'C'D'\), вершинами которого являются середины сторон данного параллелограмма.

Поставщик газа может заключить договор на транзит своего газа до клиента через любой из трёх газопроводов: Северный, Центральный или Восточный. Длина Северного газопровода равна 380 километрам, длина Центрального газопровода равна 410 километрам, а длина Восточного газопровода равна 320 километрам. Транспортировка 1000 кубометров газа на 100 километров по Северному газопроводу стоит 9 долларов, по Центральному газопроводу — 8,5 долларов, по Восточному газопроводу — 10 долларов. Сколько долларов придётся заплатить за самый выгодный транзит 1,5 миллионов кубометров газа?

Найдите корень уравнения \(9^{x-2} = 81\).

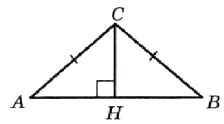
В треугольнике \(ABC AC = BC = 5, AB = 8\). Найдите \(tg A\).

Найдите значение выражения \(\frac{60}{6^{log_{6}5}}\)

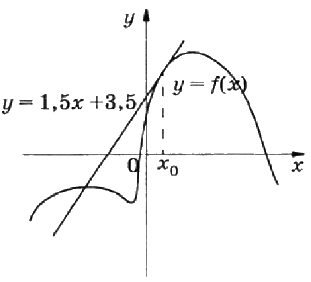
На рисунке изображён график функции \(y = f(x)\) и касательная к этому графику, проведённая в точке \(x_{0}\). Уравнение касательной дано на рисунке. Найдите значение производной функции \(y = 2f(x) - 1\) в точке \(x_{0}\)

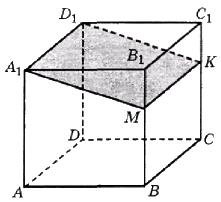
В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) известны рёбра: \(AA_1 = 6, AB = 7\), \(AD = \sqrt{53}\)- Найдите площадь сечения параллелепипеда плоскостью \(A_1MK\), где точки \(M\) и \(K\) разбивают рёбра \(BB_1\) и \(CC_1\) в отношении 2:1, считая от прямой \(BC\).

В сборнике билетов по математике всего 25 билетов, в 9 из них встречается вопрос о свойствах логарифмов. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о свойствах логарифмов.

Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 5 раз, а высоту оставить прежней?

Автомобиль разгоняется с места с постоянным ускорением \(\alpha = 0,2 m/c^2\) и через некоторое время достигает скорости \(v = 7 m/c^2\). Какое расстояние к этому моменту прошёл автомобиль? Ответ выразите в метрах.
Скорость \(v\), пройденный путь \(l\), время разгона \(t\) и ускорение \(a\)связаны соотношениями: \(v = at, l =\frac{at^2}{2}\)

Велосипедист отправился с некоторой скоростью из города \(A\) в город \(B\), расстояние между которыми равно 88 км. Возвращаясь из \(B\) в \(A\), он ехал поначалу с той же скоростью, но через один час пути вынужден был сделать остановку на 15 мин. После этого он продолжил путь в \(A\), увеличив скорость на 2 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из \(A\) в \(B\). Найдите скорость велосипедиста на пути из \(A\) в \(B\).

Найдите наименьшее значение функции

\(y = (x^{2} - 7x + 7)e^{x-5}\)

на отрезке \(\left[4; 6\right]\).