ЕГЭ Математика (профиль) 2013 Вариант 8
Вопрос B1 #939
В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт пирога с черносливом. Для пирога на 9 человек, кроме всего прочего, следует взять 0,3 фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 12 человек? Считайте, что 1 фунт равен 0,4 кг.
Вопрос B2 #940
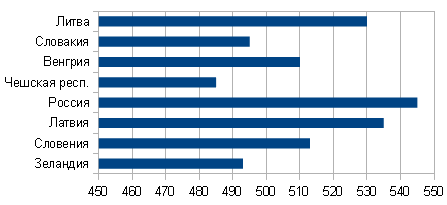
На диаграмме показан средний балл участников 8 стран в тестировании учащихся 4-го класса по математике в 2007 году (по 1000-балльной шкале).
По данным диаграммы определите, сколько стран, в которых средний балл отличается не больше, чем на 20 от среднего балла венгерских участников (саму Венгрию не считайте).
По данным диаграммы определите, сколько стран, в которых средний балл отличается не больше, чем на 20 от среднего балла венгерских участников (саму Венгрию не считайте).
Вопрос B3 #938
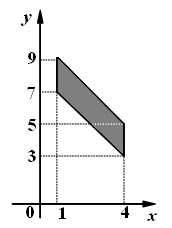
Найдите площадь параллелограмма, вершины которого имеют координаты (1; 7), (4; 3), (4; 5), (1; 9).
Вопрос B4 #937
Рейтинговое агентство определяет рейтинги автомобилей на основе оценок безопасности \(S\), комфорта \(C\), функциональности \(F\), качества \(Q\) и дизайна \(D\), Каждый показатель оценивается читателями журнала по 5-балльной шкале. Рейтинг \(R\) вычисляется по формуле
\(R= \frac{3S+2C+2F+2Q+D}{50}\)
В таблице даны оценки каждого показателя для трёх моделей автомобилей. Определите, какой автомобиль имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.| Модель автомобиля |
Безопасность | Комфорт | Функцио- нальность |
Качество | Дизайн |
| А | 3 | 4 | 4 | 3 | 5 |
| Б | 4 | 3 | 4 | 4 | 3 |
| В | 5 | 2 | 3 | 3 | 2 |
Вопрос B5 #933
Найдите корень уравнения \(4^{2-x}=64\).
Вопрос B6 #934
В треугольнике \(ABC AC = BC = 12, sin B = \frac {\sqrt{15}}{4} \). Найдите \(AB\).
Вопрос B7 #935
Найдите значение выражения \(log_{8}176 - log_{8}2,75\).
Вопрос B8 #936
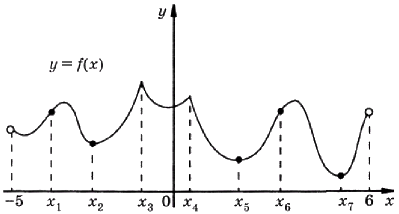
Функция \(y = f(x)\) определена на интервале (-5; 6). На рисунке изображён график функции \(у = f(x)\). Найдите среди точек \(x_{1}, x_{2}, ... , x_{7}\) те точки, в которых производная функция \(f(x)\) равна нулю. В ответ запишите количество найденных точек.
Вопрос B9 #932
В кубе \(ABCDA_{1}B_{1}C_{1}D_{1}\) точки \(K\) и \(M\) лежат на рёбрах \(BB_{1} и B_{1}C_{1}\) соответственно, причем
\( \frac{B_{1}M}{B_{1}C_{1}}= \frac{B_{1}K}{B_{1}B}=0,6\).
Найдите угол между прямыми \(KM\) и \(AC\). Ответ дайте в градусах.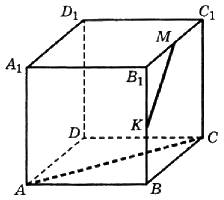
Вопрос B10 #931
Два завода выпускают одинаковые автомобильные предохранители. Первый завод выпускает 40% предохранителей, второй — 60%. Первый завод выпускает 4% бракованных предохранителей, а второй — 3%. Найдите вероятность того, что случайно выбранный в магазине предохранитель окажется бракованным.
Вопрос B11 #929
Шар объёмом 8 м3 вписан в цилиндр. Найдите объем цилиндра (в м3).
Вопрос B12 #930
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \(F_{A} = \alpha \rho gr^{3}\), где \(\alpha =4,2\) — постоянная, \(r\) — радиус аппарата в метрах, \(\rho = 1000 кг/м^{3}\) — плотность воды, a g — ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 14406000 Н? Ответ выразите в метрах.
Вопрос B13 #928
На изготовление 48 деталей первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 96 таких же деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час делает второй рабочий?
Вопрос B14 #927
Найдите наибольшее значение функции
\(y = 28 tg x - 28x + 7\pi-9\)
на отрезке \(\left [ -\frac{\pi}{4};\frac{\pi}{4} \right ]\).