ЕГЭ Математика (профиль) 2013 Вариант 5

Бегун пробежал 800 м за 2 минуты 40 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.

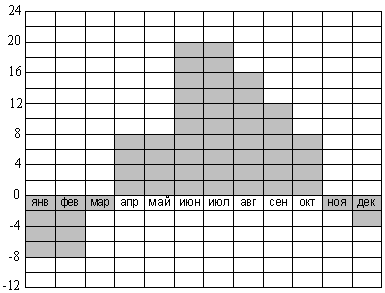
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, какой из месяцев первого полугодия был самым тёплым. В ответ напишите номер месяца.

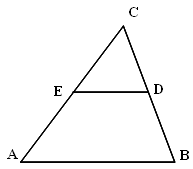
Площадь треугольника ABC равна 28. DE — средняя линия. Найдите площадь трапеции ABDE.

Для остекления музейных витрин требуется заказать 50 одинаковых стёкол в одной из трёх фирм. Площадь каждого стекла 0,35 \(м^{2}\). В таблице приведены цены на стекло и на резку стёкол. Сколько рублей будет стоить самый дешёвый заказ?

Фирма	Цена стекла (руб. за 1 м2)	Резка стекла (руб. за одно стекло)	Дополнительные  условия
A	320	20	-
B	310	25	-
C	340	15	При заказе на сумму больше 7000 руб. резка бесплатно

Найдите корень уравнения \(3^{2-2x}=81\).

В треугольнике \(ABC \angle C=90^{0}, AB=18, cos A=0,5\). Найдите \(АС\).

Найдите значение выражения \(6 ^{2+log_{6}13}\).

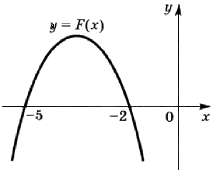
На рисунке изображён график некоторой функции \(у = f(x)\). Одна из первообразных этой функции равна \(F(x) = -\frac{1}{3}x^{3}-\frac{7}{2}x^{2}-10x-6\).
Найдите площадь закрашенной фигуры.

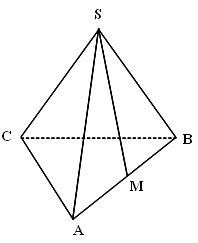
В правильной треугольной пирамиде \(SABC\) \(M\) — середина ребра \(AB, S\) — вершина. Известно, что \(BC = 4\), а площадь боковой поверхности пирамиды равна \(18\). Найдите длину отрезка \(SM\).

На соревнования по метанию ядра приехали 5 спортсменов из Сербии, 7 из Хорватии и 3 из Норвегии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать спортсмен из Норвегии.

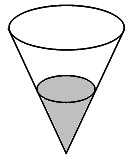
В сосуд, имеющий форму конуса, налили 20 мл жидкости до половины высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?

Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности \(I\), оперативности \(S\), объективности \(T\) публикаций, а также качества сайта \(Q\). Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 0 до 4.
Аналитики, составляющие формулу рейтинга, считают, что информативность ценится вчетверо, а оперативность и объективность публикаций — втрое дороже, чем качество сайта. Таким образом, формула приняла вид \(R=\frac{4I+3S+3T+Q}{A}\).
Каким должно быть число \(A\), чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 100?

Два велосипедиста одновременно отправились в 153-километровый пробег. Первый ехал со скоростью, на 8 км/ч большей, чем скорость второго, и прибыл к финишу на 8 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.

Найдите наименьшее значение функции
\(y=9 cos x + 10x + 8\)
на отрезке \(\left [ 0; \frac{3\pi}{2} \right ]\)