ЕГЭ Математика (профиль) 2013 Вариант 2
Вопрос B1 #843
Авторучка в магазине стоит 19 рублей. Сколько рублей заплатит покупатель за 70 авторучек, если при покупке больше 50 авторучек магазин делает скидку 10% от стоимости всей покупки?
Вопрос B2 #844
На рисунке жирными точками показана цена унции золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену золота на момент закрытия торгов в указанный период (в долларах США за унцию).

Вопрос B3 #845
Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
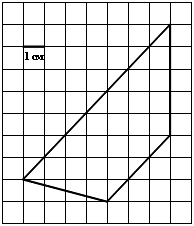
Вопрос B4 #846
В таблице даны тарифы на услуги трёх фирм такси. Предполагается поездка длительностью 90 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ?
*Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки.
| Фирма такси | Подача машины | Продолжительность и стоимость минимальной поездки* | Стоимость 1 минуты сверх продолжительности минимальной поездки |
| А | 250руб. | Нет | 12 руб. |
| Б | Бесплатно | 15 мин — 225руб. | 13 руб. |
| В | 200 руб. | 10 мин — 200руб. | 12 руб. |
Вопрос B5 #847
Найдите корень уравнения \(log_{2}(7-x)=5\)
Вопрос B6 #848
На окружности отмечены точки \(А, В\) и \(С\). Дуга окружности \(АС\), не содержащая точку В, составляет \(130^o\). Дуга окружности \(ВС\), не содержащая точку \(А\), составляет \(72^o\). Найдите вписанный угол \(АСЕ\). Ответ дайте в градусах.

Вопрос B7 #849
Найдите \(sin \alpha\), если \(cos\alpha=\frac{\sqrt{21}}{5}\) и \(\alpha \in \left ( \frac{3\pi }{2} ;2\pi \right )\)
Вопрос B8 #850
Материальная точка движется прямолинейно по закону \(x(t)=\frac{1}{3}t^3+5t^2+25t\), где \(х\) — расстояние от точки о
отсчёта в метрах, \(t\) — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна \(64 м/с\)?
Вопрос B9 #851
Высота конуса равна 36, а диаметр основания равен 30. Найдите длину образующей конуса.

Вопрос B10 #852
В классе 21 шестиклассник, среди них два друга — Митя и Петя. Класс случайным образом делят на три группы, по 7 человек в каждой. Найдите вероятность того, что Митя и Петя окажутся в одной и той же группе.
Вопрос B11 #853
Во сколько раз увеличится объём правильного тетраэдра, если все его рёбра увеличить в восемь раз?
Вопрос B12 #854
В ходе распада радиоактивного изотопа его масса \(m(t)=m_{0}2^{-\frac{t}{T}}\), где \(m_0\) (мг) - начальная масса изотопа, \(t\) (мин.) - время, прошедшее от начального момента, \(T\)(мин) - период полураспада изотопа. В начальный момент масса изотопа \(m_0=80\) мг. Период полураспада \(T=3\) мин. Через сколько минут масса изотопа станет равна 10 мг?
Вопрос B13 #855
Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 60%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 2%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Вопрос B14 #856
Найдите наименьшее значение функции \(y=8x^2-x^3+13\) на отрезке \(\left [ -5;5 \right ]\).