ЕГЭ Математика (профиль) 2017 Вариант 187
Вопрос B1 #3655
Расход бензина у автомобиля составлял в 2016г 11л на 100км. После замены двигателя в 2017г расход бензина уменьшился до 9л на 100 км.
На сколько процентов стоимость поездки на одно и то же расстояние стала меньше, если цена бензина осталась прежней. Ответ округлить до 0,1%
На сколько процентов стоимость поездки на одно и то же расстояние стала меньше, если цена бензина осталась прежней. Ответ округлить до 0,1%
Вопрос B2 #3656
Хозяйство закупило:
200кг картофеля по цене 25 руб/кг,
300кг по 30 руб/кг,
150кг по 40 руб/кг.
Какова средняя цена закупленного картофеля. Ответ округлить до целого числа рублей.
200кг картофеля по цене 25 руб/кг,
300кг по 30 руб/кг,
150кг по 40 руб/кг.
Какова средняя цена закупленного картофеля. Ответ округлить до целого числа рублей.
Вопрос B3 #3657
Спортсмены бегут 25 кругов по беговым дорожкам на стадионе. Длина дорожки (меряется внутренняя часть первой дорожки) равна 400м. Ширина дорожки 1 м. Спортсмен А бежит по первой дорожке, а В – по второй. На сколько метров больше пробежал спортсмен В. (Считать \(\pi=3,14\))
Вопрос B4 #3658
В школе 25% учащихся ходят в секцию волейбола, 35% - в секцию самбо, 60% не ходят ни в одну из этих секций. Найти вероятность того, что выбранный наугад школьник ходит в обе секции.
Вопрос B5 #3659
Решить уравнение \(\frac{2}{3}x - 0,75 = \frac{29}{84} - \frac{3}{7}x \)
Вопрос B6 #3660
Найти медиану, проведенную из вершины прямого угла прямоугольного треугольника с острым углом \(30 ^{\circ}\) и площадью \(8 \sqrt{3}\)
Вопрос B7 #3661
Касательная к графику функции \(y=f(x)\) в точке с абсциссой \(x_{0}\) параллельна прямой, пересекающей гиперболу \(y= \frac{6}{x+3}\) в точках с абсциссами \(x_{1}=-1\) и \(x_{2}=3\). Найти \({f}'(x_{0})\)
Вопрос B8 #3662
В правильную четырехугольную усеченную пирамиду ABCDA’B’C’D’, площадь верхнего основания которой A’B’C’D’ в 9 раз меньше площади нижнего основания ABCD, вписан шар радиуса 1. Найти площадь основания ABCD.
Вопрос B9 #3663
Найдите \(log_{a}b\), если \(log_{b}(a^{2}b)=log_{a}(ab^{8})\) (В ответе укажите решение или большее решение, если их несколько)
Вопрос B10 #3664
Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной \(l\) км с постоянным ускорением \(a км/ч^{2}\), вычисляется по формуле \(v^{2}=2la\). Найти наибольшую скорость, с которой может двигаться автомобиль, если ускорение не больше \(8000 км/ч^{2}\), а расстояние \(l\) равно \(400м\).
Вопрос B11 #3665
Концентрация полезного вещества в растворе 60%. Масса раствора 3 кг. Сколько чистой воды надо добавить, чтобы концентрация полезного вещества уменьшилась до 20%?
Вопрос B12 #3666
Найти точку минимума функции \(y=4xe^{2}-4e^{x}-x^{2}+2\)
Вопрос B13 #3667
a) Решить уравнение:
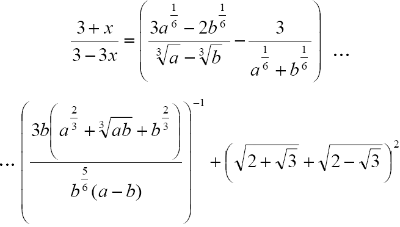
Вопрос B14 #3668
В прямой треугольной призме АВСА’B’C’, где АВ=6; АС=7; СВ=5; АА’=8, проведено сечение СМN параллельно ребру АВ, которое делит объем призмы пополам (точка М лежит на АА’, N – на ВВ’).
а) найти отношение АМ:МА’
b) Найти тангенс угла между плоскостями АВС и СMN.
а) найти отношение АМ:МА’
b) Найти тангенс угла между плоскостями АВС и СMN.
Вопрос B15 #3669
Решить неравенство
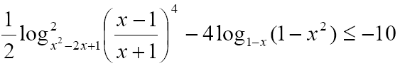
Вопрос B16 #3670
Отрезок АВ является диаметром окружности. Точки С и D окружности расположены по разные стороны от прямой АВ, длины хорд АС и BD равны 2 и 4 соответственно. Хорда CD пересекает АВ в точке Е, причем АЕ : ЕВ = 1 : 3.
а) Доказать, что если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
б) Найти радиус окружности.
а) Доказать, что если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
б) Найти радиус окружности.
Вопрос B17 #3671
Общий призовой фонд турнира по волейболу не менее 37 тыс. руб. Из него выплачиваются командам деньги купюрами по 1 тыс. руб. по следующему правилу. Команда, занявшая 1 место, получит половину фонда и еще 0,5 тыс. руб.; вторая команда – половину оставшихся денег и еще 0,5 тыс. руб.; третья – половину остатка и еще 0,5 тыс. руб. и т.д. Известно, что после выдачи денег, в кассе осталось не более 4 тыс. руб. Какое минимальное число команд могло участвовать в турнире по этим правилам?
Сколько при этом было денег в фонде, и сколько получила каждая команда, если известно, что купюры не разменивались?
Сколько при этом было денег в фонде, и сколько получила каждая команда, если известно, что купюры не разменивались?
Вопрос B18 #3672
Задана функция
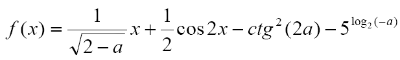
Вопрос B19 #3673
Взяли последовательность первых 15 натуральных чисел.
а) Можно ли эти числа разбить на 5 групп так, что бы суммы чисел стоящих в одной группе имели разные остатки при делении на 5?
б) Можно ли эти числа разбить на 7 групп так, что бы суммы чисел входящих в одну группу имели разные остатки при делении на 7?
в) Можно ли эти числа упорядочить таким образом, что бы сумма любых трех последовательных чисел делилась на 5?
а) Можно ли эти числа разбить на 5 групп так, что бы суммы чисел стоящих в одной группе имели разные остатки при делении на 5?
б) Можно ли эти числа разбить на 7 групп так, что бы суммы чисел входящих в одну группу имели разные остатки при делении на 7?
в) Можно ли эти числа упорядочить таким образом, что бы сумма любых трех последовательных чисел делилась на 5?