ЕГЭ Математика (профиль) 2013 Вариант 17
Вопрос B1 #1417
Каждый день во время конференции расходуется 70 пакетиков чая. Конференция длится 6 дней. Чай продается в пачках по 50 пакетиков. Сколько пачек нужно купить на все дни конференции?
Вопрос B2 #1418
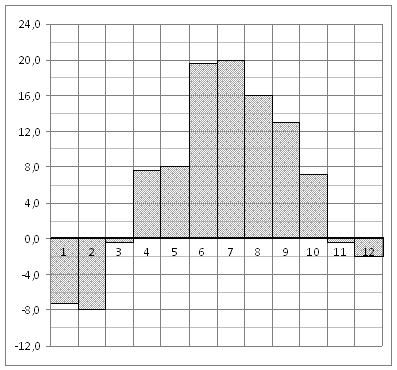
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.
Вопрос B3 #1419
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры.

Вопрос B4 #1420
В таблице даны условия банковского вклада в трех различных банках. Предполагается, что клиент кладет на счет 20000 рублей на срок 1 год. В каком банке к концу года вклад окажется наибольшим? В ответе укажите сумму этого вклада в рублях.
* В начале года или месяца со счета снимается указанная сумма в уплату за ведение счета
** В конце года вклад увеличивается на указанное количество процентов.
| Банк | Обслуживание счета* | Процентная ставка (% годовых)** |
| Банк А | 50 руб. в год | 2,2 |
| Банк Б | 9 руб. в месяц | 2,3 |
| Банк В | Бесплатно | 1,2 |
** В конце года вклад увеличивается на указанное количество процентов.
Вопрос B5 #1421
Найдите корень уравнения \(6^{3-x}=0,6\cdot 10^{3-x}\)
Вопрос B6 #1422
Сторона \(AB\) тупоугольного треугольника \(ABC\) равна радиусу описанной около него окружности. Найдите угол \(C\). Ответ дайте в градусах.

Вопрос B7 #1423
Найдите значение выражения
\(a \left( 36a^{2}-25\right) \left( \frac{1}{6a+5}-\frac{1}{6a-5}\right)\)
при \(a=36,7\)Вопрос B8 #1424
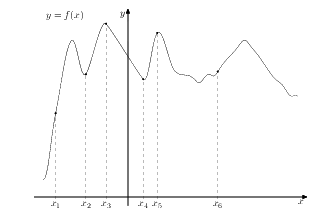
На рисунке изображён график функции \(f(x)\) и шесть точек на оси абсцисс: \(x_{1}, x_{2}, ...,x_{6}\)
В скольких из этих точек производная функции \(f(x)\) отрицательна?
В скольких из этих точек производная функции \(f(x)\) отрицательна?
Вопрос B9 #1425
В правильной треугольной пирамиде \(SABC\) \(L\) — середина ребра \(BC\), \(S\) — вершина. Известно, что \(SL=2\), а площадь боковой поверхности равна \(3\). Найдите длину отрезка \(AB\).
Вопрос B10 #1426
Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Вопрос B11 #1427
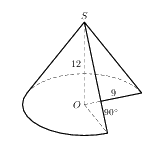
Найдите объем \(V\) части конуса, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi}\)
Вопрос B12 #1428
Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой \(m_{в}\)(в килограммах) от температуры \(t_{1}\) до температуры \(t_{2}\)(в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы \(m_{др}\) кг. Он определяется формулой \(\eta=\frac{c_{в}m_{в}(t_{2}-t_{1})}{q_{др}m_{др}}\cdot 100%\), где \(c_{в}=4,2\cdot 10^{3}\) Дж/(кг·К) — теплоёмкость воды, \(q_{др}=8,3\cdot 10^{6}\)Дж/кг — удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть \(m_{в}=83\)кг воды от \(10^{0}C\) до кипения, если известно, что КПД кормозапарника не больше \(21%\). Ответ выразите в килограммах.
Вопрос B13 #1429
Из одной точки круговой трассы, длина которой равна 32 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 119 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Вопрос B14 #1430
Найдите наименьшее значение функции \(y=\frac{x^{2}+25}{x}\) на отрезке [1;10].