ЕГЭ Математика (профиль) 2016 Вариант 155
Вопрос B1 #3226
В спортивной гимназии обучается 777 школьников. Известно, что число девочек составляет не менее 33% от числа всех учащихся гимназии. Какое наибольшее количество мальчиков может быть в этой гимназии?
Вопрос B2 #3227
На рисунке показано изменение биржевой стоимости акций нефтедобывающей компании в первой половине мая. 3 мая бизнесмен приобрёл 2000 акций этой компании. 1000 акций он продал 7 мая, а остальные акции продал 12 мая. Сколько рублей потерял бизнесмен в результате этих операций?

Вопрос B3 #3228
На рисунке клетка имеет размер 1 см х 1 см. Найдите площадь треугольника с вершинами в точках А, В и С. Ответ приведите в квадратных сантиметрах.
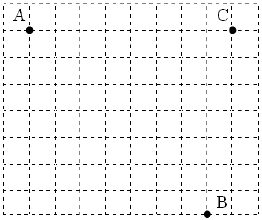
Вопрос B4 #3229
Некоторый прибор состоит из трёх блоков. Если в работе одного из блоков происходит сбой, прибор отключается. Вероятность сбоя в течение года для первого и второго блоков составляет по 0,2, а для третьего блока - 0,1. Какова вероятность, что в течение года произойдёт хотя бы одно отключение данного прибора?
Вопрос B5 #3230
Найдите корень уравнения \(\displaystyle 10^{2x+1,7}=\sqrt{0,1}\)
Вопрос B6 #3231
В трапеции \(ABCD(AB||CD)\) угол \(DCB\) равен \(72^{\circ}\). Окружность с центром в точке В проходит через точки \(A, D и C\). Найдите величину угла \(ADC\). Ответ дайте в градусах.
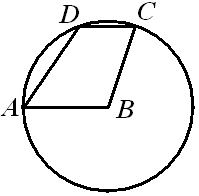
Вопрос B7 #3232
К графику функции \(y = f (x)\) в точке с абсциссой \(x_{0}\) проведена касательная, которая параллельна прямой, проходящей через точки (-1; 2) и (3; -3) этого графика. Найдите \({f}'(x_0)\).
Вопрос B8 #3233
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите объем конуса, если объем шара равен 120.
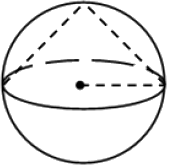
Вопрос B9 #3234
Вычислите \(\displaystyle \sqrt{12} \cdot cos^{2} \frac{5 \pi}{12} - \sqrt{3} \)
Вопрос B10 #3235
Кинетическая энергия тела, имеющего массу \(m\) (кг) и скорость \(v\) (м/с) равна \(E= \frac{mv^{2}}{2}\) (Дж). Какую наименьшую начальную скорость должна иметь пуля массой \(10\) грамм, чтобы при прохождении через неподвижную мишень передать ей энергию не меньше \(600\) Дж, уменьшив при этом свою скорость не более, чем в два раза? (Считать, что в процессе полёта пули потери энергии не происходит). Ответ дайте в м/с.
Вопрос B11 #3236
Моторная лодка проплыла против течения реки 150 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше, чем на путь против течения. Найдите скорость течения реки, если скорость лодки в неподвижной воде равна 20 км/ч. Ответ дайте в км/ч.
Вопрос B12 #3237
Найдите точку минимума функции \(f(x)=x^{3}(3x+4)-12(x^{2}+1)\) на промежутке \((-5; 0,5)\).
Вопрос B13 #3238
Дано уравнение \(\displaystyle log_{2}x^{2} + log_{x}4=5\).
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \(\displaystyle \left [ \sqrt[3]{3}; \sqrt[3]{65} \right ]\)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \(\displaystyle \left [ \sqrt[3]{3}; \sqrt[3]{65} \right ]\)
Вопрос B14 #3239
Через середину ребра \(AA_{1}\) куба \(ABCDA_{1}B_{1}C_{1}D_{1}\) перпендикулярно прямой \(BD_{1}\) проведена плоскость \(\alpha\).
А) Докажите, что сечением куба плоскостью \(\alpha\) является правильный шестиугольник.
Б) Найдите угол между плоскостями \(\alpha\) и \(ABC\).
А) Докажите, что сечением куба плоскостью \(\alpha\) является правильный шестиугольник.
Б) Найдите угол между плоскостями \(\alpha\) и \(ABC\).
Вопрос B15 #3240
Решите неравенство \(\displaystyle \sqrt{9-x^{2}} \cdot (3sinx-2cos^{2}x) \geqslant 0\)
Вопрос B16 #3241
В прямоугольный треугольник \(ABC\) вписана окружность \( \omega\), касающаяся гипотенузы \(AB\) в точке \(M\). Точка \(O\) - центр описанной около треугольника \(ABC\) окружности. Касательная к окружности \(\omega\), проведенная из точки \(O\), пересекает сторону \(AC\) в точке \(P\).
А) Докажите, что площадь треугольника \(ABC\) равна произведению длин отрезков \(AM\) и \(BM\).
Б) Найдите площадь четырехугольника \(BCPO\), если известно, что \(AM=12, BM=5\).
А) Докажите, что площадь треугольника \(ABC\) равна произведению длин отрезков \(AM\) и \(BM\).
Б) Найдите площадь четырехугольника \(BCPO\), если известно, что \(AM=12, BM=5\).
Вопрос B17 #3242
1 марта 2012 года близнецы Саша и Паша решили открыть в банке вклад на 3 года. У каждого из них имелась сумма 700 000 рублей. Саша вложил свои деньги под 10% годовых. Паша перевел все свои деньги в доллары, отдав 35 рублей за каждый доллар, и открыл валютный вклад под 1% годовых. Через три года Саша и Паша закрыли свои счета. Паша тут же решил всю снятую сумму снова перевести в рубли. Известно, что 1 марта 2015 года банк давал за 1 доллар 50 рублей. У кого из братьев в итоге на руках оказалась большая сумма? На сколько рублей?
Вопрос B18 #3243
Найдите все \(a\), при каждом из которых уравнение \(\displaystyle a \cdot 2^{x} - \frac{2^{x+1}+1}{2^{x}-1}=2a+2\) имеет ровно один корень.
Вопрос B19 #3244
А) Какое наибольшее число ладей можно поставить на шахматной доске так, чтобы никакие две не били друг друга?
Б) На шахматной доске поставлены восемь ладей. Какое наибольшее число клеток может оказаться не под боем этих ладей?
В) На 64 клетках шахматной доски выписаны подряд числа от 1 до 64 (в верхнем ряду слева направо числа от 1 до 8, во втором ряду числа от 9 до 16 и т.д.) Восемь ладей поставлены так, что никакие две не бьют друг друга. Подсчитана сумма чисел, написанных на тех восьми клетках, на которых поставлены ладьи. Найдите все значения, которые может принимать эта сумма.
Б) На шахматной доске поставлены восемь ладей. Какое наибольшее число клеток может оказаться не под боем этих ладей?
В) На 64 клетках шахматной доски выписаны подряд числа от 1 до 64 (в верхнем ряду слева направо числа от 1 до 8, во втором ряду числа от 9 до 16 и т.д.) Восемь ладей поставлены так, что никакие две не бьют друг друга. Подсчитана сумма чисел, написанных на тех восьми клетках, на которых поставлены ладьи. Найдите все значения, которые может принимать эта сумма.