ЕГЭ Математика (профиль) 2016 Вариант 149

В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

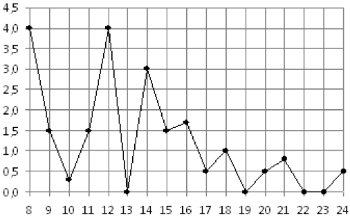
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало меньше 2 миллиметров осадков.

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Двое играют в кости - они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну, то наступает ничья. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того, что он выиграет.

Найдите корень уравнения \(\sqrt{6-4x-x^{2}}= x+ 4\). Если корней несколько, то в ответе укажите их сумму.

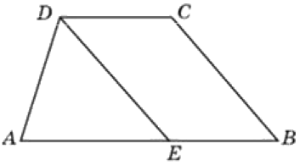
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

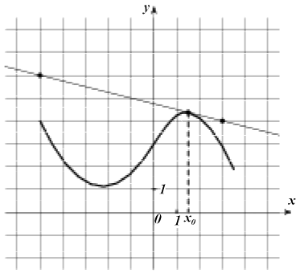
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_{0}\). Найдите значение производной функции \(f(x)\) в точке

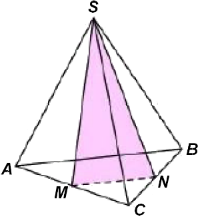
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Найдите \(61a-11b+50\), если \(\displaystyle \frac{2a-7b+5}{7a-2b+5}=9\)

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону \(U=U_{0}sin(\omega t + \varphi )\), где \(t\) — время в секундах, амплитуда \(U_{0}=2 В\), частота \(\omega = 120 ^{\circ}/c\), фаза \(\varphi=-30^{\circ}\). Датчик настроен так, что если напряжение в нём не ниже чем \(1 В\), загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 12 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.

Найдите наименьшее значение функции \(\displaystyle y=(x+3)^{2} e^{-3-x}\) на отрезке \([-5;-1]\)

Дано уравнение \(\displaystyle 2^{|x-2|sinx} = (\sqrt{2})^{x|sinx|}\)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \(\left [-\pi;\frac{\pi}{2} \right ]\)

В правильной четырехугольной пирамиде \(FABCD\) с основанием \(ABCD\) все ребра равны \(5\). Точки \(M,\:N\) лежат на ребрах \(BC\) и \(CD\) соответственно, причем \(CM=3,\:DN=2\). Плоскость \(\alpha\) проходит через точки \(M,\: N\) и параллельна прямой \(FC\).
А) Докажите, что плоскость \(\alpha\) перпендикулярна ребру \(AF\)
Б) Вычислите площадь сечения пирамиды плоскостью \(\alpha\)

Решите неравенство:

\(2 log_{x+4} (2x+7) \cdot log_{4x^{2}+28x+49} (2-x) + log_{\frac{1}{x+4}}(x^{2}-5x+6)\geqslant 0\)

Через вершины \(A,B,C\) параллелограмма \(ABCD\) со сторонами \(AB=3\) и \(BC=5\) проведена окружность, пересекающая прямую \(BD\) в точке \(E\), причем \(BE=9\).
А) Докажите, что \(BE>BD\)
Б) Найдите диагональ \(BD\)

Автофургон грузоподъемностью 339 кг перевозит ящики с виноградом и яблоками. Вес и стоимость ящика с виноградом составляют 15 кг и 10 у.е., ящика с яблоками – 27 кг и 8 у.е. соответственно. Известно, что количество загруженных на автофургон ящиков с виноградом составляет не более 70% от количества загруженных ящиков с яблоками. Определите наибольшую возможную суммарную стоимость всех ящиков с виноградом и яблоками, перевозимых автофургоном при данных условиях.

При каких значениях параметра \(a\) система

\(\displaystyle \begin{cases}|x+a|+|y-a|+|a+1+x|+|a+1-y|=2 \\ y=2|x-4|-5 \end{cases}\)

имеет единственное решение?

а) Можно ли занумеровать рёбра куба натуральными числами от 1 до 12 так, чтобы для каждой вершины куба сумма номеров рёбер, которые в ней сходятся, была одинаковой?
б) Аналогичный вопрос, если расставлять по рёбрам куба числа –6, –5, –4, –3, –2, –1, 1, 2, 3, 4, 5, 6.