ЕГЭ Математика (профиль) 2016 Вариант 148
Вопрос B1 #2892
На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака. Цена бензина 31 руб. 20 коп. за литр. Клиент получил 1 руб. 60 коп. сдачи. Сколько литров бензина было залито в бак?
Вопрос B2 #2893
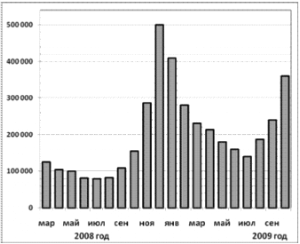
На диаграмме показано количество запросов со словом СНЕГ, сделанных на поисковом сайте Yandex.ru во все месяцы с марта 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество запросов за данный месяц. Определите по диаграмме наименьшее месячное количество запросов со словом СНЕГ с января по октябрь 2009 года.
Вопрос B3 #2894
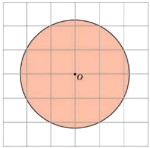
Найдите площадь \(S\) круга, считая стороны квадратных клеток равными \(1\). В ответе укажите \(\frac{s}{\pi}\).
Вопрос B4 #2895
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70% этих стекол, вторая — 30%. Первая фабрика выпускает 5% бракованных стекол, а вторая — 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Вопрос B5 #2896
Найдите корень уравнения \(\frac{1}{\sqrt{3-x}}=\frac{1}{x-1}\). Если корней несколько, то в ответе укажите их сумму.
Вопрос B6 #2897
Стороны четырехугольника \(ABCD\) \(AB, BC, CD\) и \(AD\) стягивают дуги описанной окружности, градусные величины которых равны соответственно \(95, 49, 71, 145\) градусов. Найдите угол \(B\) этого четырехугольника. Ответ дайте в градусах.

Вопрос B7 #2898
Прямая \(y=4x-2\) является касательной к графику функции \(ax^{2}+28x+14\). Найдите \(a\) .
Вопрос B8 #2899
Найдите объем многогранника, вершинами которого являются точки \(A,B,C,A_{1},C_{1}\) правильной треугольной призмы \(ABCA_{1}B_{1}C_{1}\), площадь основания которой равна \(3\), а боковое ребро равно \(2\).
Вопрос B9 #2900
Найдите значение выражения \(\frac{9^{x+11} \cdot 2^{3x+8}}{3^{2x+21} \cdot 4^{x+4}}\) при \(x=2\)
Вопрос B10 #2901
Плоский замкнутый контур площадью \(S = 0,5 м^{2}\) находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой \(\varepsilon_{i}=aScos \alpha\), где \(\alpha\) - острый угол между направлением магнитного поля и перпендикуляром к контуру, \(a=4 \cdot 10^{-4} Тл/с\) — постоянная, \(S\) - площадь замкнутого контура, находящегося в магнитном поле (в \(м^{2}\)). При каком минимальном угле \(\alpha\)(в градусах) ЭДС индукции не будет превышать \(10^{-4}В\)?
Вопрос B11 #2902
Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?
Вопрос B12 #2903
Найдите точку минимума функции \(y=4x-4ln(x+7)+6\)
Вопрос B13 #2904
Дано уравнение \(\sqrt{1-cos2x}=sin2x\).
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[- \frac{3\pi}{2};0 \right ]\).
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[- \frac{3\pi}{2};0 \right ]\).
Вопрос B14 #2905
Все ребра правильной четырехугольной пирамиды \(FABCD\) с основанием \(ABCD\) равны \(7\). Точки \(P,Q,R\) лежат на ребрах \(FA, AB, BC\) соответственно, причем \(FP=BR=4,AQ=3\).
А) Докажите, что плоскость \(PQR\) перпендикулярна ребру \(FD\)
Б) Найдите расстояние от вершины \(D\) до плоскости \(PQR\)
А) Докажите, что плоскость \(PQR\) перпендикулярна ребру \(FD\)
Б) Найдите расстояние от вершины \(D\) до плоскости \(PQR\)
Вопрос B15 #2906
Решите неравенство \(log_{5}(2+x)(x-5)>log_{25}(x-5)^{2}\)
Вопрос B16 #2908
В окружность радиуса \(R\) вписан четырехугольник \(ABCD\), \(P\) – точка пересечения его
диагоналей, \(AB=CD=5, AD>BC\). Высота , опущенная из точки \(B\) на сторону \(AD\), равна \(3\), а площадь треугольника \(ADP\) равна \(\frac{}{}\).
А) Докажите, что \(ABCD\) – равнобедренная трапеция
Б) Найдите стороны \(AD, BC\) и радиус окружности \(R\).
А) Докажите, что \(ABCD\) – равнобедренная трапеция
Б) Найдите стороны \(AD, BC\) и радиус окружности \(R\).
Вопрос B17 #2909
Строительной организации необходимо построить некоторое количество одинаковых домов общей площадью \(2500 м^{2}\). Стоимость одного дома площадью \(a м^{2}\) складывается из стоимости материалов \(p_{1}a^{3/2}\) тыс.руб, стоимости строительных работ \(p_{2}a\) тыс.руб и стоимости отделочных работ \(p_{3}a^{1/2}\) тыс.руб. Числа \(p_{1},p_{2},p_{3}\) являются последовательными членами геометрической прогрессии, их сумма равна \(21\), а их произведение равно \(64\). Если построить \(63\) дома, то затраты на материалы будут меньше, чем затраты на строительные и отделочные работы. Сколько следует построить домов, чтобы общие затраты были минимальными?
Вопрос B18 #2907
Найдите все значения \(a\), при каждом из которых система уравнений
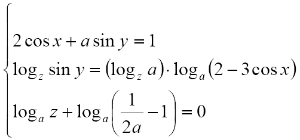
Вопрос B19 #2910
а) На доске записаны числа: 4, 14, 24, ... , 94, 104. Можно ли стереть сначала одно число из записанных, потом стереть еще два, потом – еще три, и, наконец, стереть еще четыре числа так, чтобы после каждого стирания сумма оставшихся на доске чисел делилась на 11?
б) В строку выписано 23 натуральных числа (не обязательно различных). Докажите, что между ними можно так расставить скобки, знаки сложения и умножения, что значение полученного выражения будет делиться на 2000 нацело.
б) В строку выписано 23 натуральных числа (не обязательно различных). Докажите, что между ними можно так расставить скобки, знаки сложения и умножения, что значение полученного выражения будет делиться на 2000 нацело.