ЕГЭ Математика (профиль) 2016 Вариант 141
Вопрос B1 #2854
Сегодня в зоомагазине по акции продается корм для кошек "Whiskas" со скидкой 30%. Сколько стоил один пакетик "Whiskas" до акции, если сегодня шесть таких пакетиков можно было купить за 105 рублей? Ответ дайте в рублях.
Вопрос B2 #2855
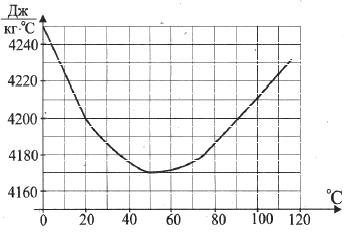
На графике показано изменение удельной теплоёмкости водного раствора некоторого вещества в зависимости от температуры. По горизонтали указывается температура в градусах Цельсия, по вертикали – удельная теплоёмкость в \(\frac{Дж}{кг \cdot ^{\circ}C}\). Определите по рисунку, на сколько изменится удельная теплоемкость при нагревании раствора с \(20^{\circ}\) до \(100^{\circ}\). Ответ дайте в \(\frac{Дж}{кг \cdot ^{\circ}C}\)
Вопрос B3 #2856
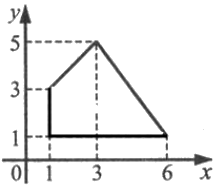
Найдите площадь четырехугольника, изображенного на рисунке.
Вопрос B4 #2857
По преданию, когда-то среди юношей существовало гадание. Один из парней зажимал в руке 10 стальных прутиков так, чтобы их концы торчали сверху и снизу, а другой юноша связывал эти прутики попарно между собой сверху и снизу. Если при этом все десять прутиков оказывались связанными в одно кольцо, то это должно было означать, что юноша в текущем году женится. Какова вероятность того, что связанные прутики будут образовывать кольцо? Ответ округлите до сотых.
Вопрос B5 #2858
Найдите сумму корней уравнения \(\sqrt[3]{2x-3}=2x-3\).
Вопрос B6 #2859
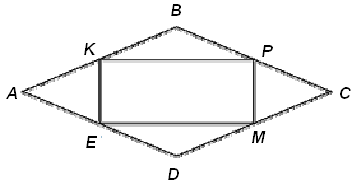
В ромбе \(ABCD\) точки \(K, P, M, E\) – середины его сторон. Определите угол (в градусах) между диагоналями четырехугольника \(KPME\), если известно, что угол \(B\) ромба равен \(136^{\circ}\)
Вопрос B7 #2860
К графику функции \(y = f (x)\) в точке \(A(2,5; 1,2)\) ее графика проведена касательная. Определите ординату точки пересечения касательной с осью \(Oy\), если известно, что значение производной \(f'(x)\) в точке \(A\) равно \(0,75\).
Вопрос B8 #2861
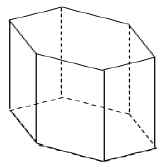
Объем правильной шестиугольной призмы равен 180. Сначала каждое ее боковое ребро увеличили в два раза, а затем каждую сторону каждого основания уменьшили в три раза. Найдите объем полученной призмы.
Вопрос B9 #2862
Найдите значение выражения \(log_{2}^{3} (log_{3} \sqrt[4]{3})\)
Вопрос B10 #2863
При вращении ведёрка с водой на верёвке в вертикальной плоскости вода не выливается из него, если сила её давления на дно ведёрка неотрицательна во всех точках траектории. В верхней точке траектории сила давления воды на дно минимальна и равна \(P=m \left( \frac{v^{2}}{L} - g \right)\)H, где \(m\) – масса воды в кг, \(v\) – скорость движения ведёрка в м/с, \(L\) – длина веревки в метрах, \(g = 10 м/с^{2}\) – ускорение свободного падения. С какой минимальной скоростью v надо вращать ведёрко, чтобы вода не выливалась из него, если длина веревки равна \(57,6 см\)? Ответ дайте в м/с.
Вопрос B11 #2864
Три числа составляют арифметическую прогрессию. Если первые два оставить, а к третьему прибавить сумму двух первых, то полученные числа составят геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
Вопрос B12 #2865
Найдите точку минимума функции
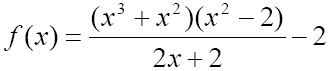
Вопрос B13 #2866
Дано уравнение \(\frac{1-4cosx}{3+4cosx}=tg^{2}x\)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие интервалу \(\left( \frac{3 \pi}{4}; 3\pi \right)\)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие интервалу \(\left( \frac{3 \pi}{4}; 3\pi \right)\)
Вопрос B14 #2867
В правильной треугольной призме \(ABCA_{1}B_{1}C_{1}\) все ребра равны между собой. Через центр верхнего основания призмы и середины двух ребер нижнего основания проведена плоскость \(\beta \).
А) Найдите угол, который образует плоскость \(\beta \) с плоскостью \(ABC\).
Б) Найдите площадь сечения призмы \(ABCA_{1}B_{1}C_{1}\) плоскостью \(\beta \), если известно, что ребро призмы равно \(6\).
А) Найдите угол, который образует плоскость \(\beta \) с плоскостью \(ABC\).
Б) Найдите площадь сечения призмы \(ABCA_{1}B_{1}C_{1}\) плоскостью \(\beta \), если известно, что ребро призмы равно \(6\).
Вопрос B15 #2868
Решите неравенство \(log_{x}(log_{2}(4^{x}-6)) \leqslant 1\)
Вопрос B16 #2869
В ромб вписана окружность \(\Theta\). Окружности \(w_{1}\) и \(w_{2}\) (разного радиуса) расположены так, что каждая касается окружности \(\Theta\) и двух соседних сторон ромба.
А) Докажите, что площадь круга, ограниченного окружностью \(\Theta\), составляет менее 80% площади ромба.
Б) Найдите отношение радиусов окружностей \(w_{1}\) и \(w_{2}\), если известно, что диагонали ромба относятся, как \(1:2\).
А) Докажите, что площадь круга, ограниченного окружностью \(\Theta\), составляет менее 80% площади ромба.
Б) Найдите отношение радиусов окружностей \(w_{1}\) и \(w_{2}\), если известно, что диагонали ромба относятся, как \(1:2\).
Вопрос B17 #2870
Эльвира взяла в кредит 1 млн. рублей на срок 36 месяцев. По договору она должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 10%, а затем уменьшается на сумму, уплаченную Эльвирой банку в конце месяца. Суммы, выплачиваемые Эльвирой, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. На сколько тысяч рублей больше Эльвира выплатит банку в течение первого года кредитования, нежели в течение третьего года?
Вопрос B18 #2871
Найдите все значения параметра \(a\), при каждом из которых уравнение \(log_{3}(ax^{3}+a) - 2log_{3} \sqrt{x+1} = log_{3}x\) имеет хотя бы один действительный корень.
Вопрос B19 #2872
А) В клетках таблицы \(3х3\) расставлены числа \(-4, -3, -2, -1, 0, 1, 2, 3, 4\). Рассмотрим восемь сумм: суммы трёх чисел в каждой строке, каждом столбце и по двум диагоналям. Могут ли все эти суммы оказаться одинаковыми?
Б) В клетках таблицы \(3х3\) расставлены числа \(–1, 0\) и \(1\) (каждое из этих чисел встречается хотя бы один раз). Рассмотрим восемь сумм: суммы трёх чисел в каждой строке, каждом столбце и по двум диагоналям. Могут ли все эти суммы оказаться различными?
В) В клетках таблицы \(3х3\) расставлены девять различных натуральных чисел. Рассмотрим восемь произведений: произведения трёх чисел в каждой строке, каждом столбце и по двум диагоналям. Могут ли все эти произведения оказаться одинаковыми?
Б) В клетках таблицы \(3х3\) расставлены числа \(–1, 0\) и \(1\) (каждое из этих чисел встречается хотя бы один раз). Рассмотрим восемь сумм: суммы трёх чисел в каждой строке, каждом столбце и по двум диагоналям. Могут ли все эти суммы оказаться различными?
В) В клетках таблицы \(3х3\) расставлены девять различных натуральных чисел. Рассмотрим восемь произведений: произведения трёх чисел в каждой строке, каждом столбце и по двум диагоналям. Могут ли все эти произведения оказаться одинаковыми?