ЕГЭ Математика (профиль) 2013 Вариант 14

Банка краски стоит 160 рублей. Какое наибольшее число таких банок можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?

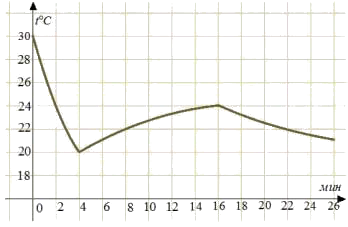
На графике показано изменение температуры в компьютерном классе после включения кондиционера. На оси абсцисс откладывается время в минутах, на оси ординат — температура в градусах Цельсия. По графику определите, сколько градусов составляла температура воздуха в компьютерном классе в момент включения кондиционера.

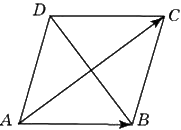
Диагонали ромба \(ABCD\) равны 12 и 16. Найдите длину вектора \(\overrightarrow{AB}-\overrightarrow{AC}\).

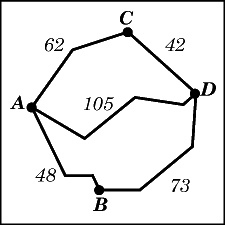
Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 44 км/ч, через пункт С едет автобус со средней скоростью 52 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 42 км/ч. На рисунке показана схема дорог и расстояние (в км) между пунктами по дорогам.

Все три автомобиля одновременно выехали из А. Какой автомобиль добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.

Найдите наименьший корень уравнения

\( 3log_{8}^{2}(5x+7)-7log_{8}(5x+7)+2=0\)

Катеты равнобедренного прямоугольного треугольника равны \(2+\sqrt{2}\). Найдите радиус окружности, вписанной в этот треугольник.

Найдите значение выражения

\(\sqrt[3]{5+\sqrt{3}+\sqrt{12-6\sqrt{3}}}\)

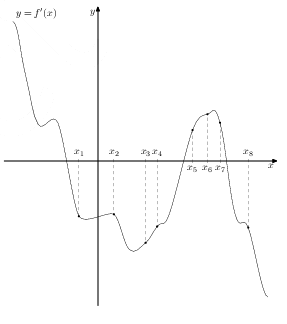
На рисунке изображён график \(y=f'(x)\) производной функции \(f(x)\) и восемь точек на оси абсцисс: \(x_{1},x_{2},...,x_{8}\)

В скольких из этих точек функция \(f(x)\) убывает?

В правильной шестиугольной призме \(ABCDEFA_1B_1C_1D_1E_1F_1\) все ребра равны 1. Найдите расстояние между точками \(A\) и \(E_1\) .

Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.

Основанием прямой треугольной призмы \(ABCA_1B_1C_1\) является равнобедренный треугольник \(ABC\), в котором \(AB=AC=5, BC=6\). Боковое ребро призмы равно 10 . Точка \(P\) принадлежит ребру \(AA_1\), причем \(PA_1=4AP\). Найдите тангенс угла между плоскостями \(BCP\) и \(BCC_1\).

Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной \(l\) км с постоянным ускорением a \(км/ч^{2}\), вычисляется по формуле \(v^{2}=2la\). Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 5000 \(км/ч^{2}\). Ответ выразите в км/ч.

По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 85 км/ч и 50 км/ч. Длина пассажирского поезда равна 600 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Найдите наименьшее значение функции

\(y=3x-ln(x+3)^{3}\)

на отрезке [-2,5;5]