ЕГЭ Математика (профиль) 2016 Вариант 138
Вопрос B1 #2797
Три землекопа за два часа выкопают три ямы. Сколько ям выкопают шесть землекопов за пять часов?
Вопрос B2 #2798
В таблице приведена статистика набранных очков на тай-брейке волейбольного
матча между "Белогорьем" и казанским "Зенитом". Определите, сколько
розыгрышей мяча на тай-брейке происходило при равном счёте.
| "Белогорье" | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||||||||||||||
| "Зенит" | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Вопрос B3 #2799
Размер клетки 1х1. Найдите тангенс угла ABC.
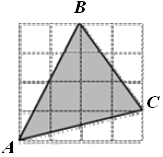
Вопрос B4 #2800
Бобчинский, Добчинский и Городничий играют в преферанс. После раздачи карт Бобчинский, заглянув незаметно в карты к Городничему, заказал мизер. Какова вероятность, что Бобчинский получит с прикупа двух тузов, если известно, что ни у него, ни у Городничего на руках тузов нет? Ответ округлите до сотых.
(При игре в преферанс используются 32 карты: от 7 до туза каждой масти. Каждому из трех игроков раздается по 10 карт, оставшиеся две - прикуп - откладываются в сторону)
Вопрос B5 #2801
Найдите корень уравнения \(ArcCos 4x + ArcCos 2x = \frac{\pi}{3}\)
Вопрос B6 #2802
Середины сторон невыпуклого четырехугольника \(ABCD\) являются вершинами четырехугольника \(KLMN\) с площадью \(12\). Найдите площадь четырехугольника \(ABCD\).
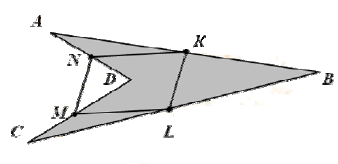
Вопрос B7 #2803
Найдите производную функции \(y=(2015x)^{2016x}\) в точке \(x_{0}= \frac{1}{2015}\)
Вопрос B8 #2804
Между двумя параллельными плоскостями заключены перпендикуляр длиной 4 м и наклонная, равная 6 м. Расстояния между их концами в каждой плоскости равны по 3 м. Найдите расстояние между серединами перпендикуляра и наклонной. Ответ дайте в метрах.
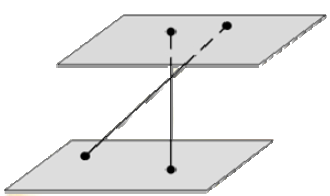
Вопрос B9 #2805
Найдите значение выражения

Вопрос B10 #2806
Автомобиль проехал половину пути со скоростью 60 км/ч, оставшуюся часть пути он половину времени двигался со скоростью 10 км/ч, а последний участок – со скоростью 20 км/ч. Какова средняя скорость автомобиля на всем пути? Ответ дайте в км/ч.
Вопрос B11 #2807
Имеется 10 ящиков. В некоторых из них лежат по 10 ящиков меньшего размера, а в некоторых из меньших ящиков лежат еще по 10 ящиков. Сколько всего ящиков, если заполненных оказалось 54? (Заполненным считается ящик, в котором находится хотя бы один ящик меньшего размера).
Вопрос B12 #2808
Найдите наименьшее значение выражения \(\frac{16x^{3}}{y} + \frac{y^{3}}{x} - \sqrt{xy}\)
Вопрос B13 #2809
Дано уравнение \(2015^{x} + 2016 \cdot 2015^{1-x} - 4031\)
a) Решите уравнение
б)Укажите корни этого уравнения, принадлежащие отрезку \([log_{2017} 2016; log_{2016} 2017]\).
a) Решите уравнение
б)Укажите корни этого уравнения, принадлежащие отрезку \([log_{2017} 2016; log_{2016} 2017]\).
Вопрос B14 #2810
На высоте равностороннего конуса как на диаметре построен шар.
А) Докажите, что полная поверхность конуса равновелика поверхности шара.
Б) Найдите отношение объема той части конуса, которая лежит внутри шара, к объему той части шара, которая лежит вне конуса.
А) Докажите, что полная поверхность конуса равновелика поверхности шара.
Б) Найдите отношение объема той части конуса, которая лежит внутри шара, к объему той части шара, которая лежит вне конуса.
Вопрос B15 #2811
Решите неравенство \(\sqrt{1+x^{2}} - x \leq \frac{5}{2 \sqrt{1 + x^{2}}}\)
Вопрос B16 #2812
На основании \(AC\) равнобедренного треугольника \(ABC\) взята точка \(E\). Окружности \(w_{1}\) и \(w_{2}\) , вписанные в треугольники \(ABE\) и \(CBE\), касаются прямой \(BE\) в точках \(K\) и \(M\) соответственно.
А) Докажите, что \(KM = \frac{1}{2} \cdot |CE - AE|\).
Б) Определите, на сколько радиус окружности \(w_{2}\) больше радиуса окружности \(w_{1}\), если известно, что \(AE=9, CE=15\), а радиус вписанной в треугольник \(ABC\) окружности равен \(4\).
А) Докажите, что \(KM = \frac{1}{2} \cdot |CE - AE|\).
Б) Определите, на сколько радиус окружности \(w_{2}\) больше радиуса окружности \(w_{1}\), если известно, что \(AE=9, CE=15\), а радиус вписанной в треугольник \(ABC\) окружности равен \(4\).
Вопрос B17 #2813
Имеется две одинаковых по объёму банки: первая с мёдом, а вторая с дёгтем. Шутник взял ложку дёгтя из второй банки и добавил её в банку с мёдом. Перемешав содержимое в первой банке, шутник перелил такую же ложку смеси во вторую банку. Потом он проделал всё это ещё раз: из второй банки перелил ложку полученной смеси в первую, после чего из первой банки перелил ложку новой смеси во вторую. Определите, чего оказалось больше: дегтя в мёде или мёда в дёгте?
Вопрос B18 #2814
Найдите все значения параметра \(a\), при каждом из которых система уравнений

Вопрос B19 #2815
Используя каждую из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 по одному разу, составьте такие два пятизначных числа, чтобы
А) их разность была наибольшей;
Б) их разность была по модулю наименьшей;
В) их произведение было наибольшим.
А) их разность была наибольшей;
Б) их разность была по модулю наименьшей;
В) их произведение было наибольшим.