ЕГЭ Математика (профиль) 2016 Вариант 136
Вопрос B1 #2777
Николай решил подсчитать, сколько денег он будет экономить, если бросит курить. Известно, что ежедневно Николай выкуривает пачку сигарет, которая стоит 60 рублей. Определите, сколько рублей Николай сэкономит за 4 года?
Вопрос B2 #2774
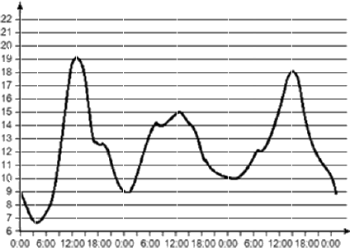
На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов четверга. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Определите по графику разность между наибольшей и наименьшей температурой в пятницу. Ответ дайте в градусах Кельвина.
Вопрос B3 #2775
Найдите угол между векторами \(\vec{a}\{ \sqrt{3};0\}\) и \( \vec{b}\{2;-2 \sqrt{3}\} \). Ответ дайте в градусах.
Вопрос B4 #2776
Команда бобслеистов состоит из четырех человек. Если хотя бы один спортсмен заболеет, то команда не выходит на старт. Вероятность заболеть для первого участника команды составляет 0,1, для второго – 0,2, а для третьего – 0,3, а для четвертого – 0,4. Какова вероятность, что команда бобслеистов не выйдет на старт?
Вопрос B5 #2772
Найдите корень уравнения \(log_{-x} (x^{2}+6x+6)=1\). Если корней несколько, то в ответе укажите их сумму.
Вопрос B6 #2773
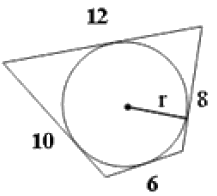
В четырехугольник со сторонами \(6, 10, 12\) и \(8\) (рисунок) вписана окружность. Найдите площадь четырехугольника, если радиус \(r\) окружности равен \(\frac{11}{3}\).
Вопрос B7 #2771
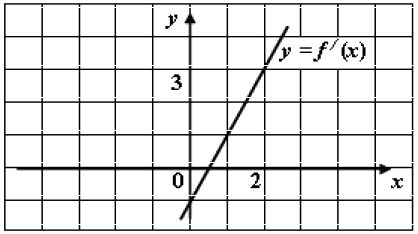
Функция \(f (x)\) определена при всех действительных \(x\). На рисунке изображен график \(f'(x)\) её производной. Найдите значение выражения \(f(3)-f(-6)\).
Вопрос B8 #2770
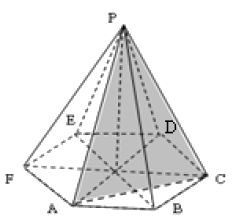
\(PABCDEF\) – правильная шестиугольная пирамида. Известно, что объем многогранника с вершинами в точках \(P, A, B\) и \(C\) равен \(12\). Найдите объем многогранника с вершинами в точках \(P, A, C, D, E\) и \(F\).
Вопрос B9 #2769
Найдите значение выражения \(\frac{12 \cdot cos 48^{\circ} \cdot cos 138^{\circ}}{sin 8^{\circ}}\)
Вопрос B10 #2768
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием \(f = 30 см\). Расстояние \(d_{1}\) от линзы до лампочки может изменяться в пределах от \(20\) до \(40\) см, а расстояние \(d_{2}\) от линзы до экрана – в пределах от \(180\) до \(200\) см. Изображение на экране будет четким, если выполнено соотношение \(\frac{1}{d_{1}}+ \frac{1}{d_{2}}=\frac{1}{f}\). Укажите, на каком наибольшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было чётким. Ответ выразите в сантиметрах.
Вопрос B11 #2765
Фермер в октябре продавал картофель в два раза дешевле, чем в марте. При этом выручка от продажи картофеля в октябре оказалась на 53% ниже по сравнению с мартом. Определите, на сколько процентов меньше картофеля продал фермер в октябре, чем в марте?
Вопрос B12 #2766
Найдите наибольшее значение функции \(f(x)=18-\sqrt[6] {x^{2}-12x+100}\).
Вопрос B13 #2767
Дано уравнение \(3 \cdot 16 ^{sin x cos x}=2 \cdot 9^{sin 2x}\)
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку \( \left [ \frac{\pi}{4}; \frac{3 \pi}{2} \right ] \)
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку \( \left [ \frac{\pi}{4}; \frac{3 \pi}{2} \right ] \)
Вопрос B14 #2764
В прямоугольном параллелепипеде \(ABCDA_{1}B_{1}C_{1}D_{1}\) \(AB=3, AA_{1}=4, AD=5\).
А) Докажите, что точки \(B, C_{1}, D\) и \(A_{1}\) не лежат в одной плоскости.
Б) Найдите объем многогранника с вершинами в точках \(B, C_{1}, D\) и \(A_{1}\).
А) Докажите, что точки \(B, C_{1}, D\) и \(A_{1}\) не лежат в одной плоскости.
Б) Найдите объем многогранника с вершинами в точках \(B, C_{1}, D\) и \(A_{1}\).
Вопрос B15 #2762
Решите неравенство:
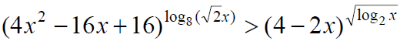
Вопрос B16 #2763
В выпуклом четырехугольнике \(ABCD\) диагонали \(AC\) и \(BD\) пересекаются в точке \(O\). Площади треугольников \(AOB\) и \(COD\) равны.
А) Докажите, что точки \(A\) и \(D\) одинаково удалены от прямой \(BC\).
Б) Найдите площадь треугольника \(AOB\), если известно, что \(AB=13, BC=10,\) \(CD=15, DA=24\).
А) Докажите, что точки \(A\) и \(D\) одинаково удалены от прямой \(BC\).
Б) Найдите площадь треугольника \(AOB\), если известно, что \(AB=13, BC=10,\) \(CD=15, DA=24\).
Вопрос B17 #2761
Три завода выпускают одинаковую продукцию. Известно, что ежегодный объём продукции на первом заводе составляет треть от суммы ежегодных объёмов продукции на втором и третьем заводах, а объём продукции на втором заводе составляет восьмую часть от суммы ежегодных объёмов на первом и третьем заводах. Найдите отношение суммы ежегодных объёмов продукции, выпускаемых на первом и втором заводах, к ежегодному объёму продукции, выпускаемой на третьем заводе.
Вопрос B18 #2760
Найдите все значения \(a\), при каждом из которых система
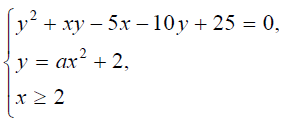
Вопрос B19 #2759
Про натуральные числа а, b и с известно, что
Б) Может ли произведение чисел \(a\) и \(c\) равняться квадрату числа \(b\)?
В) Найдите наименьшее из возможных значений выражения \(\frac{abc}{ab+bc+ca}\)
\(10 \leqslant a \leqslant 24, 25 \leqslant b \leqslant 35, 60 \leqslant c \leqslant 70 \)
А) Может ли сумма чисел \(a\) и \(b\) равняться числу \(c\)?Б) Может ли произведение чисел \(a\) и \(c\) равняться квадрату числа \(b\)?
В) Найдите наименьшее из возможных значений выражения \(\frac{abc}{ab+bc+ca}\)