ЕГЭ Математика (профиль) 2016 Вариант 135
Вопрос B1 #2740
В школе французский язык изучают 391 человек, что составляет 17% учащихся. Сколько человек в школе не изучают французский язык?
Вопрос B2 #2741
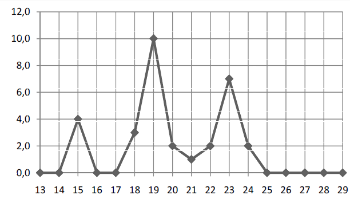
На рисунке жирными точками показано суточное количество осадков, выпадавших в Москве с 13 по 29 ноября 2015 года (с округлением до целого числа). По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 20 по 29 января включительно. Ответ дайте в миллиметрах.
Вопрос B3 #2742
Найдите площадь четырёхугольника \(ABCD\) , если точки имеют следующие координаты: \(A(46; 59) , B(47; 6
2) , C (54; 59) , D(47; 6
6) \).
2) , C (54; 59) , D(47; 6
6) \).
Вопрос B4 #2743
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, при втором выстреле – 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,95?
Вопрос B5 #2744
Найдите корень уравнения
\(\frac{2}{x^{2}-7x}= \frac{3}{5x-18}\)
Если уравнение имеет более одного корня, в ответе укажите больший из них.Вопрос B6 #2745
В треугольнике \(ABC\) угол \(C\) равен \(90^{\circ} , AC=18, tg \alpha =0,5 \). Найдите \(BC\) .
Вопрос B7 #2746
На рисунке изображён график функции \(y=f(x)\), определённой на интервале \((-9; 12)\) . Найдите сумму точек экстремума функции \(f(x)\).

Вопрос B8 #2747
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 7, а высота – 9. Найдите объем параллелепипеда.
Вопрос B9 #2748
Найдите значение выражения \(3(p(2x)-4p(x+3))\), если \(p(x)=x^{2}-12x-3\).
Вопрос B10 #2749
Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону\(\varphi = \omega t = \frac{\beta t^{2}}{2}\), где \(t\) – время в минутах, \(\omega = 15^{\circ}/мин^{2}\) – начальная угловая скорость вращения катушки, а \(\beta = 3^{\circ}/мин^{2}\) – угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки \(\varphi\) достигнет \(3000^{\circ}\). Определите время после начала работы лебёдки, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.
Вопрос B11 #2750
Первый велосипедист выехал из поселка по шоссе со скоростью 17 км/ч. Через час после него со скоростью 13 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа 10 минут после этого догнал первого. Ответ дайте в км/ч.
Вопрос B12 #2751
Найдите точку максимума функции \(y=(4x-7) cos x - 4 sin x + 5\), принадлежащую промежутку \((0;\pi)\).
Вопрос B13 #2752
Дано уравнение
б) Укажите корни уравнения, принадлежащие промежутку (-2;12).
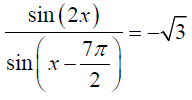
б) Укажите корни уравнения, принадлежащие промежутку (-2;12).
Вопрос B14 #2753
Все рёбра правильной треугольной призмы \(ABCA_{1}B_{1}C_{1}\) равны \(4\).
а) Постройте сечение призмы, проходящее через середины рёбер \(BC, CC_{1},A_{1}C_{1}\).
б) Найдите площадь этого сечения.
а) Постройте сечение призмы, проходящее через середины рёбер \(BC, CC_{1},A_{1}C_{1}\).
б) Найдите площадь этого сечения.
Вопрос B15 #2754
Решите неравенство
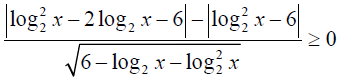
Вопрос B16 #2755
Точка \(D\) лежит на стороне \(BC\) треугольника \(ABC\).
а) Докажите, что \(AD^{2}=AB^{2} \cdot \frac{CD}{BC} + AC^{2} \cdot \frac{BD}{BC} - CD \cdot BD\).
б) Найдите площадь треугольника \(ABC\), если известно, что \(AB=14, AC=11, BD=3, AD=\sqrt{145}\).
а) Докажите, что \(AD^{2}=AB^{2} \cdot \frac{CD}{BC} + AC^{2} \cdot \frac{BD}{BC} - CD \cdot BD\).
б) Найдите площадь треугольника \(ABC\), если известно, что \(AB=14, AC=11, BD=3, AD=\sqrt{145}\).
Вопрос B17 #2756
Первая и вторая бригады, работая вместе, могут выполнить задание не более чем за 42 дня. Вторая и третья бригады, работая вместе, могут выполнить то же задание за 85 дней. Первая и третья бригады, работая вместе, могут выполнить то же задание за 55 дней. За какое минимальное целое количество дней может выполнить задание одна третья бригада?
Вопрос B18 #2757
Найдите все значения \(a\) , при каждом из которых уравнение
\((4x+2a-3)(x-2a+3)log_{4}x=0\)
имеет ровно два различных корня.Вопрос B19 #2758
а) Найдите все значения \(a\) , при каждом из которых корни уравнения \(x^{3}+9x^{2}+23x+a=0\) образуют арифметическую прогрессию.
б) Найдите все значения \(a\) , при каждом из которых уравнение \(8x^{4}-(a+37)x^{2}+2a^{2}=0\) имеет ровно четыре действительных корня, образующих арифметическую прогрессию.
в) Найдите все значения \(a\) , при каждом из которых уравнение \(x^{8}-(109a+4)x^{4}+a^{4}=0\) имеет ровно четыре действительных корня, образующих арифметическую прогрессию.
г) Числа \(cosx,- \frac{3 cos x ctg (2x)}{7}, sin x\) являются последовательными членами арифметической прогрессии. Найдите \(x\) , если известно, что один из членов этой прогрессии равен \(-0,8\) .
б) Найдите все значения \(a\) , при каждом из которых уравнение \(8x^{4}-(a+37)x^{2}+2a^{2}=0\) имеет ровно четыре действительных корня, образующих арифметическую прогрессию.
в) Найдите все значения \(a\) , при каждом из которых уравнение \(x^{8}-(109a+4)x^{4}+a^{4}=0\) имеет ровно четыре действительных корня, образующих арифметическую прогрессию.
г) Числа \(cosx,- \frac{3 cos x ctg (2x)}{7}, sin x\) являются последовательными членами арифметической прогрессии. Найдите \(x\) , если известно, что один из членов этой прогрессии равен \(-0,8\) .