ЕГЭ Математика (профиль) 2013 Вариант 12

Банка сока стоит 28 рублей. В воскресенье в магазине действует специальное предложение: заплатив за три банки, покупатель получает четыре (одна банка в подарок). Какое наибольшее количество банок такого сока можно получить на 250 рублей в воскресенье?

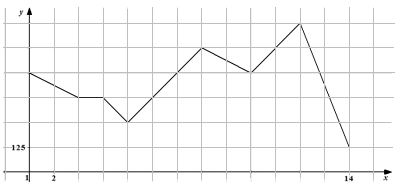
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций горнодобывающей компании в первые две недели февраля. В первую неделю февраля бизнесмен купил 12 акций, а потом продал их на второй неделе. Какую наибольшую прибыль он мог получить?

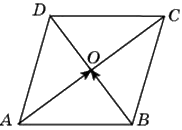
Диагонали ромба \(ABCD\) пересекаются в точке \(O\) и равны 12 и 16. Найдите длину вектора \(\overrightarrow{AO}-\overrightarrow{BO}\).

В таблице даны тарифы на услуги трёх фирм такси. Предполагается поездка длительностью 60 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ?

Фирма такси	Подача машины	Продолжительность и стоимость минимальной поездки	Стоимость 1 минуты сверх продолжительности минимальной поездки
А	200 руб.	Нет	12 руб.
Б	Бесплатно	15 мин. — 300 руб.	19 руб.
В	180 руб.	10 мин. — 200 руб.	15 руб.

Решите уравнение. Если уравнение имеет более одного корня, в ответе укажите сумму корней.

\( 2^{x}+10 \cdot \left ( \sqrt{2} \right )^{x}-144=0\)

Основания равнобедренной трапеции равны 4 и 9. Известно, что в эту трапецию можно вписать окружность. Найдите радиус этой окружности.

Найдите значение выражения \(9^{6} \cdot 7^{4} : 63^{4}\)

Материальная точка движется прямолинейно по закону где

\(x(t) = t^{2}-13t+23\),

\(x\) — расстояние от точки отсчета в метрах, \(t\) — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна \(3 м/с\)?

В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) ребро \(AB=2\), ребро \(AD =\sqrt{5}\) ребро \(AA_1=2\). Точка \(K\) — середина ребра \(BB_1\). Найдите площадь сечения, проходящего через точки \(A_1, D_1 и K\).

Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что абитуриент сможет поступить хотя бы на одну из двух упомянутых специальностей.

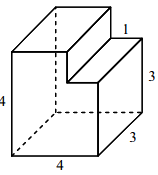
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые)

При адиабатическом процессе для идеального газа выполняется закон \(pV^{k}=const\) , где \(p\) — давление в газе в паскалях, \(V\) — объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом \( \left ( для\;него\;k=\frac{5}{3} \right )\) из начального состояния, в котором \(const=10^{5}Па\cdot м^{2}\) , газ начинают сжимать. Какой наибольший объeм \(V\) может занимать газ при давлениях \(p\) не ниже \(6 Па\)? Ответ выразите в кубических метрах.

Игорь и Паша красят забор за 35 часов. Паша и Володя красят этот же забор за 40 часов, а Володя и Игорь — за 56 часов. За сколько часов мальчики покрасят забор, работая втроем?

Найдите наибольшее значение функции

\(y=ln(11x)-11x+9\)

на отрезке \(\left [ \frac{1}{22};\frac{5}{22} \right ]\)