ЕГЭ Математика (профиль) 2015 Вариант 112
Вопрос B1 #1669
Диагональ экрана телевизора равна 145 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Вопрос B2 #1670
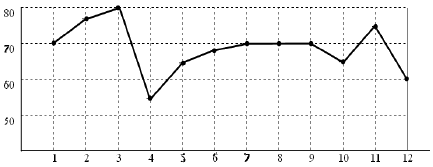
На графике точками отмечена цена (в рублях) одного килограмма масла в течение 12 месяцев 2014-го года. Для наглядности точки соединены отрезками. Определите, сколько месяцев в течение года цена на масло не превышала 70 рублей за килограмм.
Вопрос B3 #1671
При заказе дисков в некотором шведском музыкальном магазине цена одного диска не зависит от количества дисков в заказе, а доставка заказа в другие страны осуществляется на таких условиях: доставка заказа не более чем из трех дисков - 6 $; доставка заказа от 4 до 8 дисков - 15 $; доставка заказа из 9 и более дисков - 28 $. Сколько долларов придется заплатить за доставку самым дешевым способом (можно в несколько заказов) при приобретении ровно 13 дисков?
Вопрос B4 #1672
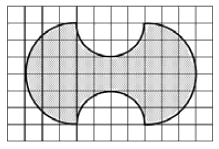
Клетка имеет размер 1 см x 1 см. Найдите площадь (в квадратных сантиметрах) фигуры, изображенной на рисунке. Ответ округлите до целых.
Вопрос B5 #1673
Сколькими способами можно поставить на шахматную доску двух королей так, чтобы никакие два не стояли под боем?
Вопрос B6 #1674
Найдите наибольший отрицательный корень уравнения \(sin 2\pi x = 1\)
Вопрос B7 #1675
Точка \(O\) – центр окружности . \(\angle BAO=24^{\circ}\), \(\angle BCO=26^{\circ}\)Найдите величину большего из углов треугольника \(ABC\).Ответ дайте в градусах.

Вопрос B8 #1676
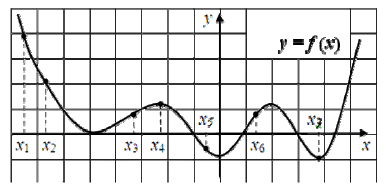
На графике дифференцируемой функции \(y = f (x)\) отмечены семь точек: \(x_{1}, x_{2}, …, x_{7}\). В какой из этих точек производная функции \(y = {f}'(x)\) принимает наименьшее значение? В ответе укажите индекс этой точки.
Вопрос B9 #1677
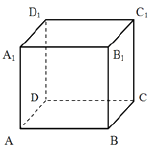
Объем куба равен 48. Найдите объем пирамиды, основанием которой является грань куба, а вершиной - центр куба.
Вопрос B10 #1678
Найдите значение выражения \(log_{0,2} \sqrt{3 \sqrt{3}-\sqrt{2}}+log_{0,2} \sqrt{3 \sqrt{3}+\sqrt{2}}\).
Вопрос B11 #1679
Бетонная плита объемом \(2 м^{3}\) погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде? (Плотность бетона равна \(2000 кг/м^{3}\), плотность воды \(1000 кг/м^{3}\), считать \(g=9,8 Н/кг\)). Ответ дайте в килоньютонах.
Вопрос B12 #1680
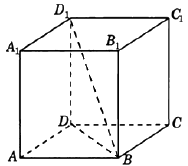
Сторона основания правильной четырехугольной призмы \(ABCDA_{1}B_{1}C_{1}D_{1}\) равна \(2 \sqrt{2}\), а боковое ребро равно \(3\). Найди косинус угла, который образует с плоскостью основания диагональ \(BD_{1}\).
Вопрос B13 #1681
Две машинистки, работая вместе, печатают в час 44 страницы текста. Первые 25% двухсотстраничной рукописи печатала первая машинистка, затем к ней присоединилась вторая, а последние 20% текста печатала только вторая машинистка. Сколько страниц в час печатает вторая машинистка, если на перепечатывание всей рукописи ушло 6 ч 40 мин, а первая машинистка работает медленнее второй?
Вопрос B14 #1682
Прямая \(y=x\) касается параболы \(y=x^{2}+bx+c\) в точке \((1; 1)\). Найдите значение \(b\).