ЕГЭ Математика (профиль) 2015 Вариант 105
Вопрос B1 #1571
Необходимо перевезти 52 одинаковых ящика весом 450 килограмм каждый. Сколько рейсов понадобится сделать для этого, используя машину грузоподъемностью 2,5 тонны?
Вопрос B2 #1572
Кондитерская фабрика выпустила в продажу два новых сорта конфет – Люкс и Шарм. На графиках показано, как эти конфеты продавались в течение года. (По горизонтальной оси откладывается время, прошедшее с начала продаж, в месяцах; по вертикальной – количество проданных за это время конфет, в тыс. тонн.) Сколько всего конфет этих двух сортов (в тыс. тонн) было продано за первые девять месяцев?
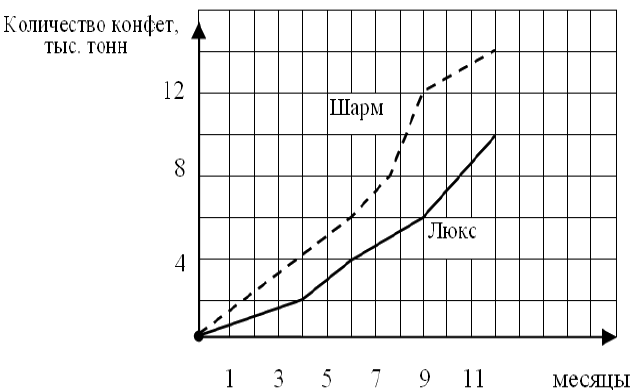
Вопрос B3 #1573
Пятиклассница Изольда Кукушкина планирует на каникулах съездить с родителями к бабушке в Самару. Из Воронежа в Самару можно ехать или поездом, или на своей машине. Билет на поезд стоит 1450 руб. на одного взрослого человека и 50% стоимости – на школьника. Автомобиль в среднем расходует 9 литров бензина на 100 км пути. Расстояние по шоссе равно 1450 км, а цена бензина равна 28 руб. за литр. Во сколько рублей обойдётся самая дешёвая поездка?
Вопрос B4 #1574
Площадь большого круга равна 24. Найдите площадь закрашенной фигуры.

Вопрос B5 #1575
В коробке лежат два чёрных, два белых и один красный шар. Из коробки наугад вынимают два шара. Какова вероятность, что вынутые шары окажутся одного цвета?
Вопрос B6 #1576
Найдите корень уравнения \(\frac{1}{2x-9}=\frac{1}{3-2x}\).
Вопрос B7 #1577
Окружность, вписанная в прямоугольный треугольник, делит точкой касания гипотенузу на отрезки 12 и 5. Найдите радиус окружности
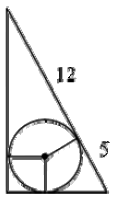
Вопрос B8 #1578
На графике функции \(y = f (x)\) отмечены семь точек с абсциссами \(-7, -5, -3, -2, 1, 2, 5\). Определите по данному графику, в какой из этих точек значение производной \({f}' (x)\) наибольшее. (В ответе укажите абсциссу этой точки).
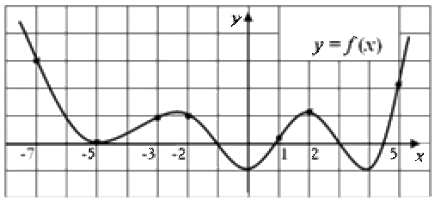
Вопрос B9 #1579
В кубе \(ABCDA_1B_1C_1D_1\) расстояние от середины ребра \(BB_1\) до точки пересечения диагоналей верхнего основания равно \(2\sqrt{3}\). Найдите объем куба.
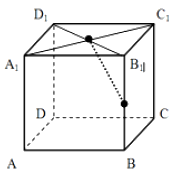
Вопрос B10 #1580
Вычислите \(8\cdot (sin \frac{\pi}{12}cos \frac{\pi}{12}-1)\)
Вопрос B11 #1581
Расстояние (в километрах) от наблюдателя, находящегося на высоте \(h\) километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле \(l = \sqrt{2Rh}\) , где \(R = 6400 км\) – радиус Земли. С какой высоты горизонт виден на расстоянии \(16\) километров? Ответ выразите в километрах.
Вопрос B12 #1582
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите радиус шара, если длина образующей конуса равна \(3\sqrt{2}\) .
Вопрос B13 #1583
Из пункта А в пункт В вышел пешеход. Одновременно с этим из пункта В в пункт А выехал велосипедист. Велосипедист прибыл в пункт А на 15 минут раньше, чем пешеход прибыл в пункт В. Определите, сколько минут затратил на путь из А в В пешеход, если известно, что с велосипедистом он встретился через 4 минуты после выхода.
Вопрос B14 #1584
Найдите точку максимума функции \(f(x)=(32-x^{2})\cdot (\sqrt{-x})^{4}\).