ЕГЭ Математика (профиль) 2015 Вариант 104

В университетскую библиотеку привезли новые учебники по геометрии для 1-3 курсов, по 280 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 6 полок, на каждой полке помещается 24 учебника. Сколько книжных шкафов можно полностью заполнить купленными учебниками?

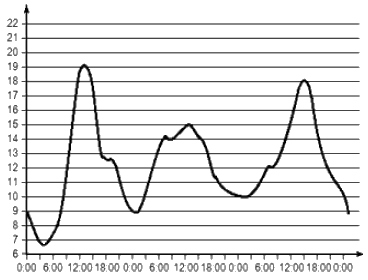
На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов понедельника. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Определите по графику наибольшую температуру воздуха в среду.

23 февраля в магазине «Все для мужчин» действует 20% скидка на одежду, 30% – на обувь и 40% – на аксессуары. При этом купить со скидкой можно не более двух товаров. Иван Иванович хочет приобрести рубашку по цене 1800 руб., туфли за 3600 руб. и запонки за 1000 руб. В каком случае Иван Иванович заплатит за свою покупку меньше всего:
1) если купит со скидкой рубашку и запонки, а туфли – без скидки;
2) если купит со скидкой рубашку и туфли, а запонки – без скидки;
3) если купит со скидкой туфли и запонки, а рубашку – без скидки?
В ответ запишите, сколько рублей заплатит Иван Иванович за покупку в этом случае.

На рисунке клетка имеет размер \(1 см х 1 см\). Найдите площадь треугольника \(ABC\). Ответ дайте в квадратных сантиметрах.

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежат 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Найдите корень уравнения \(log_{x^{2}}(6-5x)=1\). Если корней несколько, в ответе укажите больший из них.

Найдите радиус окружности, описанной около треугольника со сторонами \(3, 7\) и \(2\sqrt{10}\) .

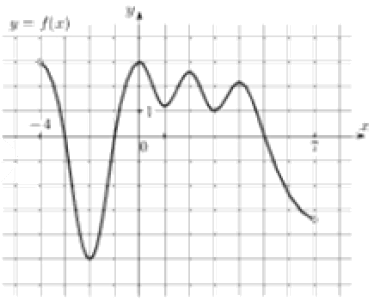
На рисунке изображен график функции \(y = f (x)\) , определенной на интервале \((-4; 7)\). Найдите количество точек, в которых производная функции \(f (x)\) равна \(0\) .

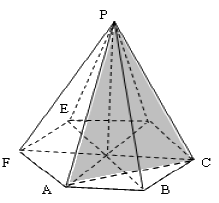
В правильной шестиугольной пирамиде \(PABCDEF\) сторона основания равна \(2\), а боковое ребро равно \(\sqrt{6}\). Найдите площадь сечения пирамиды плоскостью \(PAC\).

Найдите наименьшее значение выражения \(2\sqrt{3} cos \beta -2sin \beta -6\)

При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону \(l=l_{0}\sqrt{1-\frac{v^2}{c^2}}\) , где \(l_{0}=5м\) – длина покоящейся ракеты, \(c=3\cdot 10^5 км/с\) – скорость света, а \(v\) – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы её наблюдаемая длина стала не более \(4 м\)? Ответ выразите в км/с.

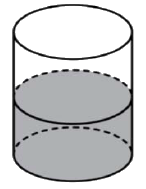
В цилиндрический сосуд налили \(2000 см^3\) воды. Уровень жидкости оказался равным \(12\) см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на \(9\) см. Чему равен объем детали? Ответ выразите в \(см^3\).

Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В выходит катер. Встретив плот, катер сразу поворачивает и идет вниз по течению реки. Какую часть всего пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?

Найдите максимальную длину промежутка, на котором функция \(f(x)=x^2 \cdot e^x\) убывает.