Каталог заданий ЕГЭ.
Задание #3231

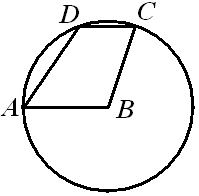
В трапеции \(ABCD(AB||CD)\) угол \(DCB\) равен \(72^{\circ}\). Окружность с центром в точке В проходит через точки \(A, D и C\). Найдите величину угла \(ADC\). Ответ дайте в градусах.