Каталог заданий ЕГЭ.
Результаты поиска - Математика (профиль).
Задания: B8
Вопрос B8 #936 Математика (профиль)
Функция \(y = f(x)\) определена на интервале (-5; 6). На рисунке изображён график функции \(у = f(x)\). Найдите среди точек \(x_{1}, x_{2}, ... , x_{7}\) те точки, в которых производная функция \(f(x)\) равна нулю. В ответ запишите количество найденных точек.
Подробнее Узнать ответ Комментировать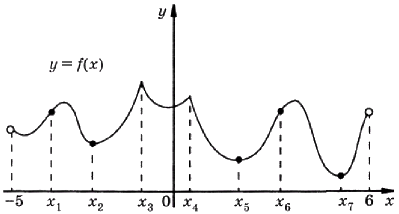
Вопрос B8 #920 Математика (профиль)
На рисунке изображён график производной функции \(f(x)\), определённой на интервале (-8; 4). Найдите точку экстремума функции \(f(x)\) на отрезке \([-7; 0]\)
Подробнее Узнать ответ Комментировать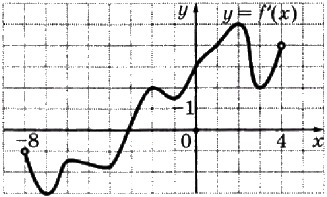
Вопрос B8 #906 Математика (профиль)
На рисунке изображен график функции \(у = f(x)\). Прямая, проходящая через точку (-2; 4), касается этого графика в точке с абсциссой 2. Найдите \(f'(2)\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #892 Математика (профиль)
На рисунке изображён график некоторой функции \(у = f(x)\). Одна из первообразных этой функции равна \(F(x) = -\frac{1}{3}x^{3}-\frac{7}{2}x^{2}-10x-6\).
Найдите площадь закрашенной фигуры.
Подробнее Узнать ответ КомментироватьНайдите площадь закрашенной фигуры.
Вопрос B8 #878 Математика (профиль)
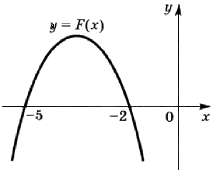
На рисунке изображен график первообразной \(y = F(x)\) некоторой функции \(у = f(x)\), определенной на интервале \((-16; -2)\). Пользуясь рисунком, определите количество решений уравнения \(f(x) = 0\) на отрезке \([-14;-8]\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #864 Математика (профиль)
На рисунке изображён график функции \(у = f(x)\) и касательная к этому графику, проведённая в точке с абсциссой 4. Найдите значение производной функции \(y = f(x)\) в точке \(х_{0} =4\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #850 Математика (профиль)
Материальная точка движется прямолинейно по закону \(x(t)=\frac{1}{3}t^3+5t^2+25t\), где \(х\) — расстояние от точки о
отсчёта в метрах, \(t\) — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна \(64 м/с\)?
Подробнее Узнать ответ КомментироватьВопрос B8 #836 Математика (профиль)
На рисунке изображён график дифференцируемой функции \(y = f(x)\). На оси абсцисс отмечены девять точек: \(x1, x2, x3, ..., x9\). Среди этих точек найдите все точки, в которых производная функции \(f(x)\) отрицательна. В ответе укажите количество найденных точек.
Подробнее Узнать ответ Комментировать
Вопрос B8 #948 Математика (профиль)
На рисунке изображён график функции \(y = f(x)\) и касательная к этому графику, проведённая в точке \(x_{0}\). Уравнение касательной дано на рисунке. Найдите значение производной функции \(y = 2f(x) - 1\) в точке \(x_{0}\)
Подробнее Узнать ответ Комментировать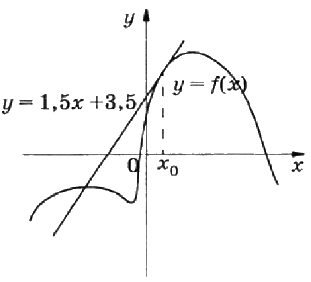
Вопрос B8 #962 Математика (профиль)
На рисунке изображён график функции \(y = f(x)\) и касательная к этому графику, проведённая в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #976 Математика (профиль)
На рисунке изображён график некоторой функции \(y = f(x)\). Пользуясь рисунком, вычислите определённый интеграл \(\int_{1}^{6}f(x)dx\)
Подробнее Узнать ответ Комментировать
Вопрос B8 #1354 Математика (профиль)
Материальная точка движется прямолинейно по закону где
Подробнее Узнать ответ Комментировать\(x(t) = t^{2}-13t+23\),
\(x\) — расстояние от точки отсчета в метрах, \(t\) — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна \(3 м/с\)?Вопрос B8 #1368 Математика (профиль)
На рисунке изображён график функции \(y =F(x)\) — одной из первообразных некоторой функции \(f (x)\) , определённой на
интервале \((-2;4)\). Пользуясь рисунком, определите количество решений уравнения \(f (x) = 0\) на отрезке \([-1;3]\) .
Подробнее Узнать ответ Комментировать
Вопрос B8 #1382 Математика (профиль)
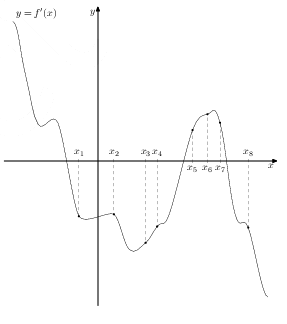
На рисунке изображён график \(y=f'(x)\) производной функции \(f(x)\) и восемь точек на оси абсцисс: \(x_{1},x_{2},...,x_{8}\)
Подробнее Узнать ответ КомментироватьВ скольких из этих точек функция \(f(x)\) убывает?
Вопрос B8 #1396 Математика (профиль)
На рисунке изображен график функции \(y=f(x)\) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Подробнее Узнать ответ Комментировать
Вопрос B8 #1410 Математика (профиль)
на рисунке изображен график \(y=f`(x)\) производной функции \(f(x)\) и шесть точек на оси абсцисс \(x_1,x_2,..,x_6\). В скольких из этих точек функция \(f(x)\) убывает?
Подробнее Узнать ответ Комментировать
Вопрос B8 #1424 Математика (профиль)
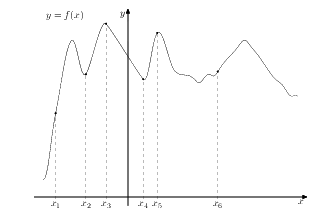
На рисунке изображён график функции \(f(x)\) и шесть точек на оси абсцисс: \(x_{1}, x_{2}, ...,x_{6}\)
В скольких из этих точек производная функции \(f(x)\) отрицательна?
Подробнее Узнать ответ КомментироватьВ скольких из этих точек производная функции \(f(x)\) отрицательна?
Вопрос B8 #1438 Математика (профиль)
На рисунке изображён график дифференцируемой функции \(y=f(x)\). На оси абсцисс отмечены девять точек: \(x_{1} , x_{2} , ..., x_{9}\) . Среди этих точек найдите все точки, в которых производная функции \(f(x)\) отрицательна. В ответе укажите количество найденных точек.
Подробнее Узнать ответ Комментировать
Вопрос B8 #1452 Математика (профиль)
Найдите площадь фигуры, ограниченной осью
абсцисс и одной аркой синусоиды.
Подробнее Узнать ответ Комментировать
Вопрос B8 #1466 Математика (профиль)
На рисунке изображен график \(y=f`(x)\) —
производной функции \(f (x)\) , определенной на интервале (-100; 100). Найдите количество точек максимума \(f (x)\) при отрицательных значениях её аргумента.
Подробнее Узнать ответ Комментировать
Вопрос B8 #1480 Математика (профиль)
Найдите площадь фигуры, ограниченной графиками функций \(f(x)=-3\left | x \right |\) и \( g(x)=x^4-4\)
Подробнее Узнать ответ Комментировать
Вопрос B8 #1494 Математика (профиль)
Материальная точка движется прямолинейно по закону \(x(t)=4t^3-39t^2+36t+4\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, прошедшее с начала движения. Определите, сколько времени пройдет между первой и второй остановкой этого тела. Ответ дайте в секундах
Подробнее Узнать ответ КомментироватьВопрос B8 #1508 Математика (профиль)
К графику функции \(f(x)=\frac{x^2}{2}+1\)проведены
две касательные в точках с абсциссами \(x=-2\) и \(x=3\) графика. Найдите тангенс угла между этими касательными.
Подробнее Узнать ответ Комментировать
Вопрос B8 #1522 Математика (профиль)
На рисунке приведен график функции \(y=f(x)\), определенной на отрезке \([-4; 5]\). Найдите количество точек графика функции \(y = f (x)\), касательная в которых параллельна прямой \(y = x-5\) или совпадает с ней.
Подробнее Узнать ответ Комментировать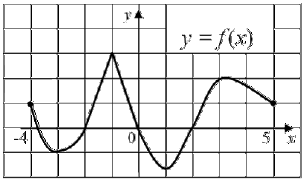
Вопрос B8 #1536 Математика (профиль)
На рисунке приведен график функции \(y=f(x)\), определенной на отрезке \([-4; 5]\). Укажите абсциссу внутренней точки области определения, в которой производная функции не существует.
Подробнее Узнать ответ Комментировать
Вопрос B8 #1550 Математика (профиль)
На рисунке изображен график функции \(y = f (x)\) , определенной на интервале \((-4; 7)\). Найдите количество точек, в которых производная функции \(f (x)\) равна \(0\) .
Подробнее Узнать ответ Комментировать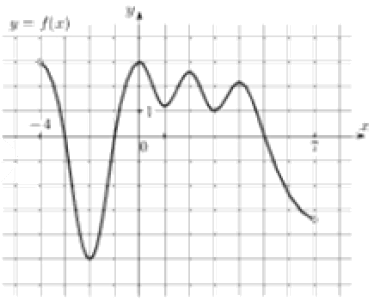
Вопрос B8 #1564 Математика (профиль)
Известно, что \(f(x)\) – нечетная периодическая функция с наименьшим положительным периодом, равным \(6\). На рисунке изображен ее график на отрезке \([-3; 0]\). Вычислите \(2f (-5) + f(10)\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #1578 Математика (профиль)
На графике функции \(y = f (x)\) отмечены семь точек с абсциссами \(-7, -5, -3, -2, 1, 2, 5\). Определите по данному графику, в какой из этих точек значение производной \({f}' (x)\) наибольшее. (В ответе укажите абсциссу этой точки).
Подробнее Узнать ответ Комментировать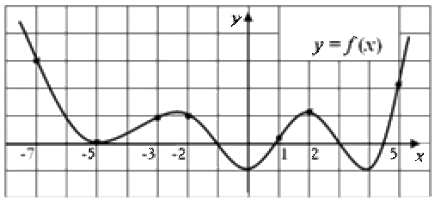
Вопрос B8 #1592 Математика (профиль)
Найдите площадь фигуры, ограниченной параболой \(y=x^2\) и прямой \(y=x+2\)
Подробнее Узнать ответ Комментировать
Вопрос B8 #1606 Математика (профиль)
К графику функции \(y = f (x)\) в точке с абсциссой \(x_{0}\) проведена касательная. Определите значение производной \({f}'(x)\) в точке \(x_{0}\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #1620 Математика (профиль)
Функция \(y = f (x)\) определена на промежутке \([-3; 5]\). На рисунке приведен график её производной. Найдите количество точек графика функции \(y = f (x)\), касательная в которых образует с положительным направлением оси абсцисс угол \(135^{\circ}\)
Подробнее Узнать ответ Комментировать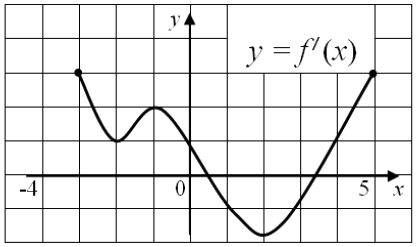
Вопрос B8 #1634 Математика (профиль)
На рисунке приведен график \(y=F(x)\) одной из первообразных функции \(f (x)\). На графике отмечены шесть точек с абсциссами \(x_1, x_2, …, x_6\). В скольких из этих точек функция \(y=f(x)\) принимает отрицательные значения?
Подробнее Узнать ответ Комментировать
Вопрос B8 #1648 Математика (профиль)
Используя геометрический смысл определенного интеграла, вычислите \(\frac{1}{\pi }\int_{0}^{2} \sqrt{4x-x^{2}}dx\).
Подробнее Узнать ответ Комментировать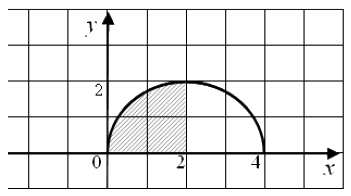
Вопрос B8 #1662 Математика (профиль)
К графику функции \(y = f (x)\) в точке с абсциссой \(x_{0}\) проведена касательная, которая параллельна прямой, проходящей через точки \((-1; 4)\) и \((3; -3)\) этого графика. Найдите \({f}'(x_{0})\).
Подробнее Узнать ответ КомментироватьВопрос B8 #1676 Математика (профиль)
На графике дифференцируемой функции \(y = f (x)\) отмечены семь точек: \(x_{1}, x_{2}, …, x_{7}\). В какой из этих точек производная функции \(y = {f}'(x)\) принимает наименьшее значение? В ответе укажите индекс этой точки.
Подробнее Узнать ответ Комментировать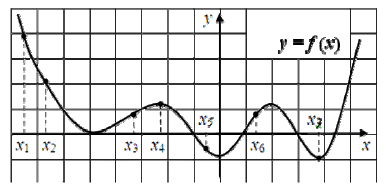
Вопрос B8 #2149 Математика (профиль)
Функция \(y = f (x)\) определена на интервале \((-4; 5)\). На рисунке приведен график её производной. Найдите промежутки возрастания функции. В ответе укажите сумму всех целых \(x\), входящих в эти промежутки.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2163 Математика (профиль)
Функция \(y = f (x)\) определена на отрезке \([-3; 5]\). На рисунке дан график её производной. Найдите количество точек минимума функции \(y = f (x)\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #2177 Математика (профиль)
По графику производной \(f'(x)\) определите количество точек минимума функции \(y = f (x)\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #2191 Математика (профиль)
На рисунке изображён график функции \(y=F(x)\) - одной из первообразных некоторой функции \(f(x)\), определённой на интервале \((-7;4)\). Пользуясь рисунком, определите количество корней уравнения \(f(x)=0\) на отрезке \([-3;2]\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #2205 Математика (профиль)
На рисунке изображен график \(y =f`(x)\) - производной функции \(f(x)\). Найдите абсциссу точки, в которой касательная к графику \(y = f (x)\) параллельна прямой \(y=2x-5\) или совпадает с ней.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2219 Математика (профиль)
Касательная к графику функции \(y= f(x)\) проходит через начало координат и точку \(M (-4; 6)\). Найдите значение производной этой функции в точке касания.
Подробнее Узнать ответ КомментироватьВопрос B8 #2233 Математика (профиль)
Найдите площадь закрашенной фигуры, ограниченной осью абсцисс и графиком функции \(f(x)=2cos2x\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #2247 Математика (профиль) <- Есть решение
Объем фужера, имеющего форму конуса, равен 240 мл. В фужер налили лимонад, при этом уровень жидкости составил \(\frac{1}{4}\) высоты. Сколько миллилитров лимонада нужно долить в фужер, чтобы он оказался полон?
Подробнее Узнать ответ Комментировать
Вопрос B8 #2266 Математика (профиль) <- Есть решение
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Подробнее Узнать ответ Комментировать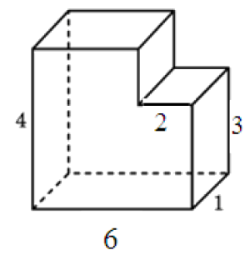
Вопрос B8 #2281 Математика (профиль) <- Есть решение
В правильной треугольной пирамиде сторона основания равна \(3\), а двугранный угол при стороне основания равен \(30 ^{\circ}\). Найдите площадь боковой поверхности пирамиды.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2300 Математика (профиль) <- Есть решение
В правильной шестиугольной пирамиде сторона основания равна \(4\sqrt{3}\), а высота равна \(8\). Через высоту пирамиды проведена плоскость. Найдите наименьшую площадь сечения пирамиды такой плоскостью.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2319 Математика (профиль) <- Есть решение
Площадь боковой поверхности конуса равна 24. Через середину его высоты параллельно основанию провели плоскость. Найдите площадь боковой поверхности усеченного конуса.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2338 Математика (профиль) <- Есть решение
В конус вписан цилиндр так, что плоскость его верхнего основания делит высоту конуса пополам. Найдите объем цилиндра, если объем конуса равен 12.
Подробнее Узнать ответ Комментировать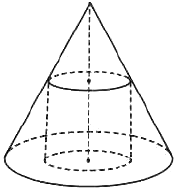
Вопрос B8 #2557 Математика (профиль) <- Есть решение
Найдите площадь поверхности правильной шестиугольной призмы, сторона основания которой равна \(\frac{5}{\sqrt [4]{3}}\), а высота – \(131 \sqrt [4]{3}\).
Подробнее Узнать ответ КомментироватьВопрос B8 #2578 Математика (профиль) <- Есть решение
Вершина \(A\) куба \(ABCDA_{1}B_{1}C_{1}D_{1}\) со стороной \(132\) является центром сферы, проходящей через точку \(A_{1}\). Найдите площадь \(S\) сферы, содержащейся внутри куба. В ответе запишите величину \(\frac{S}{\pi}\).
Подробнее Узнать ответ КомментироватьВопрос B8 #2595 Математика (профиль) <- Есть решение
В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 12. Объём цилиндра, описанного около этой пирамиды, равен \(13351 \pi\) . Найдите высоту призмы.
Подробнее Узнать ответ КомментироватьВопрос B8 #2728 Математика (профиль) <- Есть решение
Основанием прямой призмы служит прямоугольник со сторонами \(2\) и \(7\). Найдите высоту призмы, если её диагональ равна \(\sqrt{134}\) .
Подробнее Узнать ответ КомментироватьВопрос B8 #2747 Математика (профиль) <- Есть решение
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 7, а высота – 9. Найдите объем параллелепипеда.
Подробнее Узнать ответ КомментироватьВопрос B8 #2770 Математика (профиль) <- Есть решение
\(PABCDEF\) – правильная шестиугольная пирамида. Известно, что объем многогранника с вершинами в точках \(P, A, B\) и \(C\) равен \(12\). Найдите объем многогранника с вершинами в точках \(P, A, C, D, E\) и \(F\).
Подробнее Узнать ответ Комментировать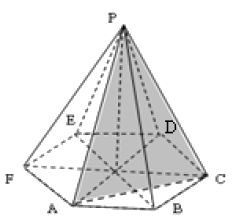
Вопрос B8 #2785 Математика (профиль) <- Есть решение
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите площадь поверхности шара, если известно, что длина образующей конуса равна \(\frac{2 \sqrt{3}}{\sqrt{2 \pi}}\)
Подробнее Узнать ответ Комментировать
Вопрос B8 #2804 Математика (профиль) <- Есть решение
Между двумя параллельными плоскостями заключены перпендикуляр длиной 4 м и наклонная, равная 6 м. Расстояния между их концами в каждой плоскости равны по 3 м. Найдите расстояние между серединами перпендикуляра и наклонной. Ответ дайте в метрах.
Подробнее Узнать ответ Комментировать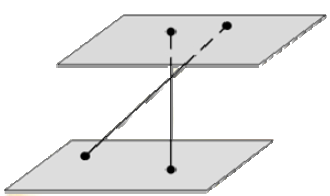
Вопрос B8 #2823 Математика (профиль) <- Есть решение
Найдите объём указанного многогранника. Все двугранные углы прямые.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2842 Математика (профиль) <- Есть решение
Радиус основания конуса равен \(5\), а косинус угла при вершине \(P\) осевого сечения равен \(\frac{12}{37}\). Найдите площадь осевого сечения конуса.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2861 Математика (профиль) <- Есть решение
Объем правильной шестиугольной призмы равен 180. Сначала каждое ее боковое ребро увеличили в два раза, а затем каждую сторону каждого основания уменьшили в три раза. Найдите объем полученной призмы.
Подробнее Узнать ответ Комментировать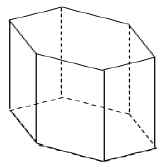
Вопрос B8 #2880 Математика (профиль) <- Есть решение
В цилиндрический сосуд положили чугунную деталь и налили 2000 см3 воды. Уровень жидкости оказался равным 21 см. Когда деталь вынули из сосуда, уровень воды понизился на 11 см. Чему равен объем детали? Ответ выразите в см3.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2899 Математика (профиль) <- Есть решение
Найдите объем многогранника, вершинами которого являются точки \(A,B,C,A_{1},C_{1}\) правильной треугольной призмы \(ABCA_{1}B_{1}C_{1}\), площадь основания которой равна \(3\), а боковое ребро равно \(2\).
Подробнее Узнать ответ КомментироватьВопрос B8 #2918 Математика (профиль) <- Есть решение
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Подробнее Узнать ответ Комментировать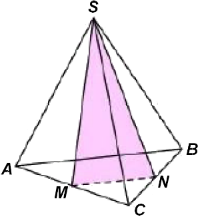
Вопрос B8 #2937 Математика (профиль) <- Есть решение
Радиус основания цилиндра равен 5, высота — 4. Найдите площадь сечения этого цилиндра плоскостью, параллельной его оси и отстоящей от нее на расстояние 3.
Подробнее Узнать ответ Комментировать
Вопрос B8 #2956 Математика (профиль) <- Есть решение
Найдите объем правильной шестиугольной призмы, каждое ребро которой равно \(2 \sqrt{3}\)
Подробнее Узнать ответ Комментировать
Вопрос B8 #2987 Математика (профиль) <- Есть решение
Найдите объем многогранника, приведенного на рисунке. Все двугранные углы прямые.
Подробнее Узнать ответ Комментировать
Вопрос B8 #3114 Математика (профиль) <- Есть решение
Прямоугольный параллелепипед \(ABCDA_{1}B_{1}C_{1}D_{1}\) имеет объём \(12\). Найдите объём пирамиды \(ABCD_{1}\).
Подробнее Узнать ответ КомментироватьВопрос B8 #3233 Математика (профиль) <- Есть решение
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите объем конуса, если объем шара равен 120.
Подробнее Узнать ответ Комментировать
Вопрос B8 #3252 Математика (профиль) <- Есть решение
Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
Подробнее Узнать ответ Комментировать
Вопрос B8 #3313 Математика (профиль) <- Есть решение
Площадь боковой поверхности правильной треугольной пирамиды \(SABC\) равна \(72\), а площадь полной поверхности пирамиды \(SMNQ\), отсекаемой от первой плоскостью, параллельной основанию и проходящей через середину высоты, равна \(24\). Найти площадь треугольника \(ABC\).
Подробнее Узнать ответ Комментировать
Вопрос B8 #3395 Математика (профиль) <- Есть решение
В треугольной пирамиде SABC точки N и M, P и Q, K и L делят соответствующие боковые ребра на 3 равные части. Объем многогранника NLQMKP равен 21. Найти объем пирамиды SABC.
Подробнее Узнать ответ Комментировать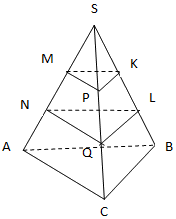
Вопрос B8 #3414 Математика (профиль) <- Есть решение
У первого цилиндра площадь полной поверхности относится к площади боковой поверхности как 5:3. У второго цилиндра радиус основания в 2 раза больше, чем у первого, а высота равна высоте первого.
Во сколько раз площадь полной поверхности второго цилиндра больше площади полной поверхности первого цилиндра.
Вопрос B8 #3643 Математика (профиль) <- Есть решение
Сечение KMLN параллельно основанию ABCD четырехугольной пирамиды SABCD и делит высоту SH в соотношении 1:3 считая от вершины S. Объем пирамиды SABCD равен 24. Найти объем пирамиды TKMLN, где точка Т принадлежит основанию ABCD.
Подробнее Узнать ответ КомментироватьВопрос B8 #3662 Математика (профиль) <- Есть решение
В правильную четырехугольную усеченную пирамиду ABCDA’B’C’D’, площадь верхнего основания которой A’B’C’D’ в 9 раз меньше площади нижнего основания ABCD, вписан шар радиуса 1. Найти площадь основания ABCD.
Подробнее Узнать ответ КомментироватьВопрос B8 #3786 Математика (профиль) <- Есть решение
Боковые грани SAB и SCD правильной четырехугольной пирамиды SABCD образуют двугранный угол 60°. Ребро основания АВ равно 1. Найти площадь полной поверхности пирамиды.
Подробнее Узнать ответ КомментироватьВопрос B8 #3805 Математика (профиль) <- Есть решение
Боковые ребра SA и SC правильной четырехугольной пирамиды SABCD взаимно перпендикулярны. SA=\(3 \sqrt{2}\). Найти объем пирамиды.
Подробнее Узнать ответ КомментироватьВопрос B8 #3824 Математика (профиль) <- Есть решение
Дана правильная шестиугольная призма \(ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}\), площадь основания которой равна \(12\), а боковое ребро равно \(6\). Найдите объем многогранника с вершинами в точках \(A,B_{1},C_{1},D_{1},E_{1},F\)
Подробнее Узнать ответ Комментировать