Каталог заданий ЕГЭ.
Результаты поиска - Математика (профиль).
Задания: B12
Вопрос B12 #930 Математика (профиль)
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \(F_{A} = \alpha \rho gr^{3}\), где \(\alpha =4,2\) — постоянная, \(r\) — радиус аппарата в метрах, \(\rho = 1000 кг/м^{3}\) — плотность воды, a g — ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 14406000 Н? Ответ выразите в метрах.
Подробнее Узнать ответ КомментироватьВопрос B12 #924 Математика (профиль)
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \(F_{A}=\alpha\rho gr^{3}\), где \(\alpha =4,2\) — постоянная, \(r\) — радиус аппарата в метрах, \(\rho = 1000 кг/м^{3}\) — плотность воды, a \(g\) — ускорение свободного падения (считайте \(g\) = 10 H/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 5250000 Н? Ответ выразите в метрах.
Подробнее Узнать ответ КомментироватьВопрос B12 #910 Математика (профиль)
Высоту над землей подброшенного вверх камня можно вычислять по формуле \(h(t) = 1,6 + 13t - 5t^{2}\), где \(t\) — время с момента броска в секундах, \(h\) — высота в метрах. Сколько секунд камень будет находиться на высоте более 6 метров?
Подробнее Узнать ответ КомментироватьВопрос B12 #896 Математика (профиль)
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности \(I\), оперативности \(S\), объективности \(T\) публикаций, а также качества сайта \(Q\). Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 0 до 4.
Аналитики, составляющие формулу рейтинга, считают, что информативность ценится вчетверо, а оперативность и объективность публикаций — втрое дороже, чем качество сайта. Таким образом, формула приняла вид \(R=\frac{4I+3S+3T+Q}{A}\).
Каким должно быть число \(A\), чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 100?
Подробнее Узнать ответ КомментироватьАналитики, составляющие формулу рейтинга, считают, что информативность ценится вчетверо, а оперативность и объективность публикаций — втрое дороже, чем качество сайта. Таким образом, формула приняла вид \(R=\frac{4I+3S+3T+Q}{A}\).
Каким должно быть число \(A\), чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 100?
Вопрос B12 #873 Математика (профиль)
Зависимость объёма спроса \(q\) (тыс. руб.) на продукцию предприятия-монополиста от цены \(p\) (тыс. руб.) задаётся формулой \(q = 85 - 5p\). Выручка предприятия за месяц \(r\) (в тыс. руб.) вычисляется по формуле \(r(p) = q \cdot p\). Определите наибольшую цену \(p\), при которой месячная выручка \(r(p)\) составит не менее 300 тыс. руб. Ответ приведите в тыс. руб.
Подробнее Узнать ответ КомментироватьВопрос B12 #868 Математика (профиль)
Компания Яндекс-Маркет вычисляет рейтинг интернет-магазинов по формуле \(R =r_{пок}-\frac{r_{пок}-r_{экс}}{(K+1)\frac{0,02K}{r_{пок}+0,1}}\)
где \(r_{пок}\) — средняя оценка магазина покупателями (от О до 1), \(r_{экс}\) — оценка магазина экспертами компании (от О до 0,7) и К — число покупателей, оценивших магазин.
Найдите рейтинг интернет-магазина «Тэта», если число покупателей, оставивших отзыв о магазине, равно 28, их средняя оценка равна 0,46, а оценка экспертов равна 0,17.
Подробнее Узнать ответ КомментироватьНайдите рейтинг интернет-магазина «Тэта», если число покупателей, оставивших отзыв о магазине, равно 28, их средняя оценка равна 0,46, а оценка экспертов равна 0,17.
Вопрос B12 #854 Математика (профиль)
В ходе распада радиоактивного изотопа его масса \(m(t)=m_{0}2^{-\frac{t}{T}}\), где \(m_0\) (мг) - начальная масса изотопа, \(t\) (мин.) - время, прошедшее от начального момента, \(T\)(мин) - период полураспада изотопа. В начальный момент масса изотопа \(m_0=80\) мг. Период полураспада \(T=3\) мин. Через сколько минут масса изотопа станет равна 10 мг?
Подробнее Узнать ответ КомментироватьВопрос B12 #840 Математика (профиль)
Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой \(h(t)=-5t^2+18t\), где \(h\) – высота в метрах, \(t\) – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров.
Подробнее Узнать ответ КомментироватьВопрос B12 #952 Математика (профиль)
Автомобиль разгоняется с места с постоянным ускорением \(\alpha = 0,2 m/c^2\) и через некоторое время достигает скорости \(v = 7 m/c^2\). Какое расстояние к этому моменту прошёл автомобиль? Ответ выразите в метрах.
Скорость \(v\), пройденный путь \(l\), время разгона \(t\) и ускорение \(a\)связаны соотношениями: \(v = at, l =\frac{at^2}{2}\)
Подробнее Узнать ответ КомментироватьСкорость \(v\), пройденный путь \(l\), время разгона \(t\) и ускорение \(a\)связаны соотношениями: \(v = at, l =\frac{at^2}{2}\)
Вопрос B12 #966 Математика (профиль)
Электрическая цепь напряжением 220B защищена предохранителем, рассчитанным на максимальную силу тока 5A. Какое наименьшее сопротивление может быть у электроприбора, включенного в эту цепь, чтобы цепь продолжала работать? Сила тока в цепи \(O\) связана с напряжением \(U\) соотношением \(i=\frac{U}{R}\) , где \(R\) —
сопротивление электроприбора. (Ответ дайте в омах.)
Подробнее Узнать ответ КомментироватьВопрос B12 #980 Математика (профиль)
Самые красивые мосты — вантовые. Вертикальные пилоны связаны огромной провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
На рисунке изображена схема одного вантового моста. Введём систему координат: ось \(Oy\) направим вертикально вдоль одного из пилонов, а ось \(Ox\) направим вдоль полотна моста, как показано на рисунке. В этой системе координат цепь моста имеет уравнение
Подробнее Узнать ответ КомментироватьНа рисунке изображена схема одного вантового моста. Введём систему координат: ось \(Oy\) направим вертикально вдоль одного из пилонов, а ось \(Ox\) направим вдоль полотна моста, как показано на рисунке. В этой системе координат цепь моста имеет уравнение
\(y=0,0061x^2-0,854x+33\),
где \(x\) к \(y\) измеряются в метрах. Найдите длину ванты, расположенной в 50 метрах от пилона. Ответ дайте в метрах.
Вопрос B12 #1358 Математика (профиль)
При адиабатическом процессе для идеального газа выполняется закон \(pV^{k}=const\) , где \(p\) — давление в газе в паскалях, \(V\) — объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом \( \left ( для\;него\;k=\frac{5}{3} \right )\) из начального состояния, в котором \(const=10^{5}Па\cdot м^{2}\) , газ начинают сжимать. Какой наибольший объeм \(V\) может занимать газ при давлениях \(p\) не ниже \(6 Па\)? Ответ выразите в кубических метрах.
Подробнее Узнать ответ КомментироватьВопрос B12 #1372 Математика (профиль)
Eмкость высоковольтного конденсатора в телевизоре \(C=2\cdot10^{-6}\)Ф. Параллельно с конденсатором подключeн резистор с сопротивлением \(R=5\cdot10^{6}\)Ом. Во время работы телевизора напряжение на конденсаторе \(U_{0}=16\)кВ. После выключения телевизора напряжение на конденсаторе убывает до \(U\)значения (кВ) за время, определяемое выражением
Подробнее Узнать ответ Комментировать\(t=\alpha R C log_{2}\frac{U_{0}}{U}\) c
, где \(\alpha=0,7\) — постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 21 с. Ответ дайте в кВ (киловольтах).Вопрос B12 #1386 Математика (профиль)
Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной \(l\) км с постоянным ускорением a \(км/ч^{2}\), вычисляется по формуле \(v^{2}=2la\). Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 5000 \(км/ч^{2}\). Ответ выразите в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B12 #1400 Математика (профиль)
Автомобиль, движущийся в начальный момент времени со скоростью \(v_{0}= 26 м/с\), начал торможение с постоянным ускорением \(a=4 м/с^{2}\). За \(t\) секунд после начала торможения он прошёл путь \(S=v_{0}t-\frac{at^{2}}{2}\)(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 60 метров. Ответ выразите в секундах.
Подробнее Узнать ответ КомментироватьВопрос B12 #1414 Математика (профиль)
На верфи проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \(F_{A}=\alpha\rho gr^{3}\), где \(\alpha=4,2\) — постоянная, r — радиус аппарата в метрах, \(\rho=1000 кг/м^3\) — плотность воды, а g — ускорение свободного падения (считайте \(g=10 H/кг\)). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
Подробнее Узнать ответ КомментироватьВопрос B12 #1428 Математика (профиль)
Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой \(m_{в}\)(в килограммах) от температуры \(t_{1}\) до температуры \(t_{2}\)(в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы \(m_{др}\) кг. Он определяется формулой \(\eta=\frac{c_{в}m_{в}(t_{2}-t_{1})}{q_{др}m_{др}}\cdot 100%\), где \(c_{в}=4,2\cdot 10^{3}\) Дж/(кг·К) — теплоёмкость воды, \(q_{др}=8,3\cdot 10^{6}\)Дж/кг — удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть \(m_{в}=83\)кг воды от \(10^{0}C\) до кипения, если известно, что КПД кормозапарника не больше \(21%\). Ответ выразите в килограммах.
Подробнее Узнать ответ КомментироватьВопрос B12 #1442 Математика (профиль)
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
\(v=c\cdot \frac{f-f_{0}}{f+f_{0}}\)
где c=1500 м/с — скорость звука в воде, \(f_{0}\)— частота испускаемого сигнала (в МГц), \(f\) — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала, если батискаф погружается со скоростью 2 м/с.
Вопрос B12 #1456 Математика (профиль)
В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_l\) известны длины ребер: \(AB=AD=3, AA_1=2\sqrt{2}\). Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки \(B, A_1 и C_1\).
Подробнее Узнать ответ Комментировать
Вопрос B12 #1470 Математика (профиль)
В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Подробнее Узнать ответ Комментировать
Вопрос B12 #1484 Математика (профиль)
В кубе \(ABCDA_1B_1C_1D_l\) длина ребра равна \(2\sqrt{2}\) . Найдите расстояние между прямыми \(CC_1\) и \(BD_1)\)
Подробнее Узнать ответ Комментировать
Вопрос B12 #1498 Математика (профиль)
Каждое ребро тетраэдра \(DABC\) равно \(2\sqrt{2}\).
Найдите расстояние между прямыми \(AB\) и \(CD\).
Подробнее Узнать ответ Комментировать
Вопрос B12 #1512 Математика (профиль)
Найдите расстояние между вершинами \(B_2 и C\) многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Подробнее Узнать ответ Комментировать
Вопрос B12 #1526 Математика (профиль)
В правильной шестиугольной пирамиде сторона основания равна \(4\sqrt{3}\) , а высота равна \(8\). Найдите длину апофемы данной пирамиды.
Подробнее Узнать ответ Комментировать
Вопрос B12 #1540 Математика (профиль)
В правильной треугольной пирамиде боковое ребро равно \(2\sqrt{13}\), апофема равна \(5\). Найдите котангенс угла, который образует боковое ребро с основанием пирамиды.
Подробнее Узнать ответ Комментировать
Вопрос B12 #1554 Математика (профиль)
В цилиндрический сосуд налили \(2000 см^3\) воды. Уровень жидкости оказался равным \(12\) см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на \(9\) см. Чему равен объем детали? Ответ выразите в \(см^3\).
Подробнее Узнать ответ Комментировать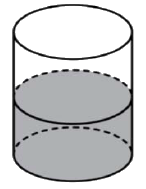
Вопрос B12 #1568 Математика (профиль)
Сторона основания правильной треугольной пирамиды равна \(6\), а высота пирамиды равна \(3\). Найдите косинус угла, который образует боковая грань с основанием пирамиды.
Подробнее Узнать ответ Комментировать
Вопрос B12 #1582 Математика (профиль)
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите радиус шара, если длина образующей конуса равна \(3\sqrt{2}\) .
Подробнее Узнать ответ Комментировать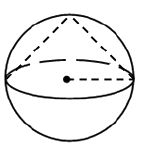
Вопрос B12 #1596 Математика (профиль)
Найдите площадь полной поверхности указанного многогранника. Все двугранные углы прямые
Подробнее Узнать ответ Комментировать
Вопрос B12 #1610 Математика (профиль)
В конусе длина образующей равна \(4 \sqrt{3}\), а угол при вершине осевого сечения равен \(120^{\circ}\). Через вершину конуса проведена плоскость. Какую наибольшую площадь может иметь сечение конуса такой плоскостью?
Подробнее Узнать ответ Комментировать
Вопрос B12 #1624 Математика (профиль)
В правильной пятиугольной пирамиде двугранный угол при стороне основания равен \(60^{\circ}\). Найдите площадь основания пирамиды, если площадь ее боковой поверхности равна \(20\).
Подробнее Узнать ответ Комментировать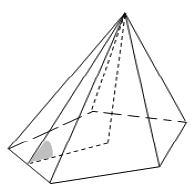
Вопрос B12 #1638 Математика (профиль)
В прямоугольном параллелепипеде \(ABCDA_{1}B_{1}C_{1}D_{1}\) \(AB=6\), \(BC=17\), \(CC_1=6\). Найдите расстояние от середины ребра \(BB_{1}\) до точки пересечения диагоналей верхнего основания параллелепипеда.
Подробнее Узнать ответ Комментировать
Вопрос B12 #1652 Математика (профиль)
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 9. Площадь полной поверхности этого параллелепипеда равна 484. Найдите третье ребро, выходящее из той же вершины.
Подробнее Узнать ответ Комментировать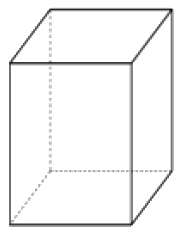
Вопрос B12 #1666 Математика (профиль)
В правильную шестиугольную призму с высотой \(6 \sqrt{3}\) вписан шар. Найдите сторону основания призмы.
Подробнее Узнать ответ Комментировать
Вопрос B12 #1680 Математика (профиль)
Сторона основания правильной четырехугольной призмы \(ABCDA_{1}B_{1}C_{1}D_{1}\) равна \(2 \sqrt{2}\), а боковое ребро равно \(3\). Найди косинус угла, который образует с плоскостью основания диагональ \(BD_{1}\).
Подробнее Узнать ответ Комментировать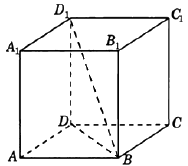
Вопрос B12 #2153 Математика (профиль)
В прямоугольном параллелепипеде ребро \(BC=4\), ребро \(AB=7\), ребро \(DD_{1}=6\). Точка \(K\) – середина ребра \(CC_{1}\). Найдите площадь сечения, проходящего через точки \(A, B\) и \(K\).
Подробнее Узнать ответ Комментировать
Вопрос B12 #2167 Математика (профиль)
В кубе \(ABCDA_1B_1C_1D_1\) длина ребра \(AB\) равна \(\sqrt[4]{12}\) . Найдите площадь сечения, проходящего через вершины \(B, C_1\) и \(D\).
Подробнее Узнать ответ Комментировать
Вопрос B12 #2181 Математика (профиль)
Найдите расстояние между точками А и В указанного на рисунке многогранника (все двугранные углы многогранника прямые).
Подробнее Узнать ответ Комментировать
Вопрос B12 #2195 Математика (профиль)
Диаметр основания конуса равен \(16\), а площадь боковой поверхности конуса равна \(136 \pi\). Найдите площадь осевого сечения этого конуса.
Подробнее Узнать ответ Комментировать
Вопрос B12 #2209 Математика (профиль)
Шар, объём которого равен \(6 \pi \), вписан в куб. Найдите объём куба.
Подробнее Узнать ответ Комментировать
Вопрос B12 #2223 Математика (профиль)
В основании прямой призмы \(ABCDA_{1}B_{1}C_{1}D_{1}\) лежит ромб \(ABCD\) с диагоналями \(AC=8\) и \(BD=6\). Боковое ребро \(AA_1\) равно \(4\). Найдите площадь полной поверхности пирамиды \(D_{1}ACD\).
Подробнее Узнать ответ Комментировать
Вопрос B12 #2237 Математика (профиль)
В прямоугольном параллелепипеде \(ABCDA_{1}B_{1}C_{1}D_{1}\) \(AB=5\), \(AD=3\), \(AA_{1}=4\). Найдите угол между прямыми \(BD_{1}\) и \(DC\). Ответ дайте в градусах.
Подробнее Узнать ответ Комментировать
Вопрос B12 #2251 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(f(x)=\frac{x^{2}+16}{x}\) на отрезке \([2;5]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2270 Математика (профиль) <- Есть решение
Найдите точку максимума функции \(y=x^{2} \cdot e^{x}\).
Подробнее Узнать ответ КомментироватьВопрос B12 #2285 Математика (профиль) <- Есть решение
Найдите наименьшее значение выражения \(x^{2}-x+y^{2}-y\).
Подробнее Узнать ответ КомментироватьВопрос B12 #2304 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(f(x)=3x^{4}+4x^{3}-12x^{2}-12\) на отрезке \([-0,5;2]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2323 Математика (профиль) <- Есть решение
Найдите точку минимума функции \(f(x)=(x^{2}-7x+10) \cdot e^{0,5x}\).
Подробнее Узнать ответ КомментироватьВопрос B12 #2342 Математика (профиль) <- Есть решение
Найдите наименьшее значение выражения \(\sqrt{(x-1)^{2}+(y-5)^{2}}+\sqrt{(x-9)^{2}+(y+10)^{2}}\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2561 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(y=x^{2} \cdot \sqrt{x} - 67,5x + 131\).
Подробнее Узнать ответ КомментироватьВопрос B12 #2575 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(y=x^{5}-5x^{3}-20x+132\) на отрезке \([1;3]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2599 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(y=x^{7} - 12,75x^{4} - 40x + 133\) на отрезке [-1;3].
Подробнее Узнать ответ КомментироватьВопрос B12 #2732 Математика (профиль) <- Есть решение
Найдите точку минимума функции \(y=\left ( x-3 \right )^{3} \left ( x-5 \right ) +134\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2751 Математика (профиль) <- Есть решение
Найдите точку максимума функции \(y=(4x-7) cos x - 4 sin x + 5\), принадлежащую промежутку \((0;\pi)\).
Подробнее Узнать ответ КомментироватьВопрос B12 #2766 Математика (профиль) <- Есть решение
Найдите наибольшее значение функции \(f(x)=18-\sqrt[6] {x^{2}-12x+100}\).
Подробнее Узнать ответ КомментироватьВопрос B12 #2789 Математика (профиль) <- Есть решение
Найдите наибольшее значение функции \(f(x)=\frac{28}{4x^{2}-28x+89}\).
Подробнее Узнать ответ КомментироватьВопрос B12 #2808 Математика (профиль) <- Есть решение
Найдите наименьшее значение выражения \(\frac{16x^{3}}{y} + \frac{y^{3}}{x} - \sqrt{xy}\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2827 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(f(x)=\frac{2}{3}x^{\frac{3}{2}} - 3x + 1\) на отрезке \([1;9]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2846 Математика (профиль) <- Есть решение
Найдите точку минимума функции \(f(x)=(x^{2}+x)^{2} - 3x^{2}\). Если точек
минимума несколько, то в ответе запишите их сумму.
Подробнее Узнать ответ КомментироватьВопрос B12 #2865 Математика (профиль) <- Есть решение
Найдите точку минимума функции
Подробнее Узнать ответ Комментировать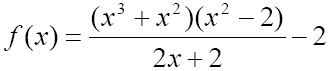
Вопрос B12 #2884 Математика (профиль) <- Есть решение
Найдите значение функции \(f(x)= \frac{x^{2}+9}{x}\) в точке максимума.
Подробнее Узнать ответ КомментироватьВопрос B12 #2903 Математика (профиль) <- Есть решение
Найдите точку минимума функции \(y=4x-4ln(x+7)+6\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2922 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(\displaystyle y=(x+3)^{2} e^{-3-x}\) на отрезке \([-5;-1]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2941 Математика (профиль) <- Есть решение
Найдите наименьшее значение функции \(\displaystyle y=x+ \frac{36}{x}\) на отрезке \([1;9]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2960 Математика (профиль) <- Есть решение
Найдите наибольшее значение функции \(\displaystyle f(x)=(x-1) \cdot e^{2x-1}\)
Подробнее Узнать ответ КомментироватьВопрос B12 #2991 Математика (профиль) <- Есть решение
К графику функции \(f(x)=\sqrt{4-x^{2}}\) в его точке с абсциссой \(x_{0}=1\) проведена касательная. Найдите угол, который образует эта касательная с положительным направлением оси абсцисс. Ответ дайте в градусах.
Подробнее Узнать ответ КомментироватьВопрос B12 #3118 Математика (профиль) <- Есть решение
Найдите наибольшее значение функции \(y=x^{2} - 4|x|\) на отрезке \([-1;3]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #3237 Математика (профиль) <- Есть решение
Найдите точку минимума функции \(f(x)=x^{3}(3x+4)-12(x^{2}+1)\) на промежутке \((-5; 0,5)\).
Подробнее Узнать ответ КомментироватьВопрос B12 #3256 Математика (профиль) <- Есть решение
Найдите наибольшее значение функции \(\displaystyle f(x)=2- \sqrt[4]{x^{2} - 10x +41}\)
Подробнее Узнать ответ КомментироватьВопрос B12 #3317 Математика (профиль) <- Есть решение
Найти наименьшее значение функции \(y= \frac{x}{3}+\frac{12}{x}\) на отрезке \([1;8]\)
Подробнее Узнать ответ КомментироватьВопрос B12 #3399 Математика (профиль) <- Есть решение
Найти наибольшее значение функции
Подробнее Узнать ответ Комментировать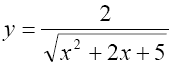
Вопрос B12 #3418 Математика (профиль) <- Есть решение
Найти наименьшее значение функции \(y=x+\frac{4}{(x-2)^{2}}\) на промежутке [0;5].
Подробнее Узнать ответ КомментироватьВопрос B12 #3647 Математика (профиль) <- Есть решение
Найти разность между наибольшим и наименьшим значениями функции:
Подробнее Узнать ответ Комментировать
Вопрос B12 #3666 Математика (профиль) <- Есть решение
Найти точку минимума функции \(y=4xe^{2}-4e^{x}-x^{2}+2\)
Подробнее Узнать ответ КомментироватьВопрос B12 #3790 Математика (профиль) <- Есть решение
Найдите точку максимума функции \(\frac{4x^{2}+9}{x}\)
Подробнее Узнать ответ КомментироватьВопрос B12 #3809 Математика (профиль) <- Есть решение
Найти наименьшее значение функции \(f(x)=\frac{1}{cos^{2}x}-6tgx + 5\)
Подробнее Узнать ответ КомментироватьВопрос B12 #3828 Математика (профиль) <- Есть решение
Найти наибольшее значение функции \(f(x)=cos \pi x - 6x\) на отрезке \( \left [ - \frac{2}{3}; 1 \right ]\)
Подробнее Узнать ответ Комментировать