Каталог заданий ЕГЭ.
Результаты поиска - Математика (профиль).
Задания: B11
Вопрос B11 #929 Математика (профиль)
Шар объёмом 8 м3 вписан в цилиндр. Найдите объем цилиндра (в м3).
Подробнее Узнать ответ КомментироватьВопрос B11 #923 Математика (профиль)
Кубик весит 800 г. Сколько граммов будет весить кубик, ребро которого в 2 раза меньше, чем ребро первого кубика, если оба кубика изготовлены из одинакового материала?
Подробнее Узнать ответ КомментироватьВопрос B11 #909 Математика (профиль)
Площадь полной поверхности данного правильного тетраэдра равна \(80 см^{2}\). Найдите площадь полной поверхности правильного тетраэдра, ребро которого в 4 раза меньше ребра данного тетраэдра. Ответ дайте в \(см^{2}\).
Подробнее Узнать ответ КомментироватьВопрос B11 #895 Математика (профиль)
В сосуд, имеющий форму конуса, налили 20 мл жидкости до половины высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Подробнее Узнать ответ Комментировать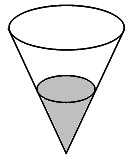
Вопрос B11 #874 Математика (профиль)
Прямоугольный параллелепипед описан около сферы радиуса 4. Найдите его объём.
Подробнее Узнать ответ Комментировать
Вопрос B11 #867 Математика (профиль)
Объём цилиндра равен 1 \(см^{3}\). Радиус основания уменьшили в 2 раза, а высоту увеличили в 3 раза. Найдите объём получившегося цилиндра. Ответ дайте в \(см^{3}\).
Подробнее Узнать ответ КомментироватьВопрос B11 #853 Математика (профиль)
Во сколько раз увеличится объём правильного тетраэдра, если все его рёбра увеличить в восемь раз?
Подробнее Узнать ответ КомментироватьВопрос B11 #839 Математика (профиль)
Объём первого цилиндра равен 12 \(м^3\). У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в \(м^3\)).
Подробнее Узнать ответ КомментироватьВопрос B11 #951 Математика (профиль)
Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 5 раз, а высоту оставить прежней?
Подробнее Узнать ответ КомментироватьВопрос B11 #965 Математика (профиль)
В правильной треугольной пирамиде \(SABC\) рёбра \(BA\) и \(BC\) разделены точками \(К\) и \(L\) так, что \(BK = BL = 4\) и \(KA = LC = 2\). Найдите угол между плоскостью основания \(ABC\) и плоскостью сечения \(SKL\). Ответ выразите в градусах.
Подробнее Узнать ответ Комментировать
Вопрос B11 #979 Математика (профиль)
Bo сколько раз увеличится объём правильного тетраэдра, если все его рёбра увеличить в шесть раз?
Подробнее Узнать ответ КомментироватьВопрос B11 #1357 Математика (профиль)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые)
Подробнее Узнать ответ Комментировать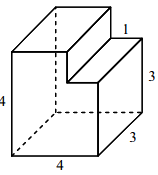
Вопрос B11 #1371 Математика (профиль)
Найдите объем многогранника, вершинами которого являются точки \(A, B, B_1, C_1\) прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\), у которого \(AB=5\), \(AD=3\), \(AA_1=4\)
Подробнее Узнать ответ КомментироватьВопрос B11 #1385 Математика (профиль)
Основанием прямой треугольной призмы \(ABCA_1B_1C_1\) является равнобедренный треугольник \(ABC\), в котором \(AB=AC=5, BC=6\). Боковое ребро призмы равно 10 . Точка \(P\) принадлежит ребру \(AA_1\), причем \(PA_1=4AP\). Найдите тангенс угла между плоскостями \(BCP\) и \(BCC_1\).
Подробнее Узнать ответ КомментироватьВопрос B11 #1399 Математика (профиль)
Найдите объем многогранника, вершинами которого являются точки \(A, B, B_{1}, C_{1}\) прямоугольного параллелепипеда \(ABCDA_{1}B_{1}C_{1}D_{1}\), у которого \(AB=5, AD=3, AA_{1}=4\).
Подробнее Узнать ответ КомментироватьВопрос B11 #1413 Математика (профиль)
Найдите объем \(V\) части цилиндра, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi}\).
Подробнее Узнать ответ Комментировать
Вопрос B11 #1427 Математика (профиль)
Найдите объем \(V\) части конуса, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi}\)
Подробнее Узнать ответ Комментировать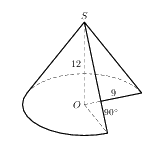
Вопрос B11 #1441 Математика (профиль)
Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.
Подробнее Узнать ответ КомментироватьВопрос B11 #1455 Математика (профиль)
В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону \(H(t)=H_0-\sqrt{2gH_0}kt+\frac{g}{2}k^2t^2\), где \(t\) – время в секундах, прошедшее с момента открытия крана, \(H_0=20 м\) – начальная высота столба воды, \(k=\frac{1}{500}\) – отношение площадей поперечных сечений крана и бака, а \(g\) – ускорение свободного падения (считайте \(g=10 м/с^2)\). Через сколько секунд после открытия крана в баке останется четверть первоначального объема воды?
Подробнее Узнать ответ КомментироватьВопрос B11 #1469 Математика (профиль)
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся по закону \(U=U_0sin(\omega t+\varphi)\) , где \(t\) – время в секундах, амплитуда \(U_0=2B\), частота \(\omega=150^{\circ}/c\), фаза \(\varphi=45\) . Датчик настроен так, что если напряжение в нем не ниже чем \(1 B\), загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Подробнее Узнать ответ КомментироватьВопрос B11 #1483 Математика (профиль)
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием \(f = 30 см\). Расстояние \(d_1\) от линзы до лампочки может изменяться в пределах от 30 до 50 см, а
расстояние \(d_2\) от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение \(\frac{1}{d_1}+\frac{1}{d_2}=\frac{1}{f}\)
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.
Подробнее Узнать ответ КомментироватьВопрос B11 #1497 Математика (профиль)
Сумма выданных кредитов, постоянно находящихся в годовом обороте банка, зависит от процентной ставки и вычисляется по формуле \(q=207-3p\) (млн. руб.), где \(p\) – величина годовой процентной ставки. Годовая прибыль банка равна разнице между суммой полученных процентов \(\frac{q\dot p}{100}\) и суммой собственных затрат банка \(f\). При каком минимальном годовом проценте банк получит прибыль 11 млн. рублей, если собственные затраты банка составят \(f = 5,2\) млн. рублей?
Подробнее Узнать ответ КомментироватьВопрос B11 #1511 Математика (профиль)
При адиабатическом процессе для идеального газа выполняется закон \(pV^k = const\), где \(p\) – давление газа в паскалях, \(V\) – объём газа в кубических метрах. В ходе
эксперимента с одноатомным идеальным газом (для него \(k=\frac{4}{3}\) из начального состояния, в котором \(const = 3,2 \cdot 10^6 Па\cdot м^4\), газ начинают сжимать. Какой наибольший объём \(V\) может занимать газ при давлении \(p\) не ниже \(2\cdot 10^5 Па\)? Ответ выразите в кубических метрах.
Подробнее Узнать ответ КомментироватьВопрос B11 #1525 Математика (профиль)
Операционная прибыль предприятия за краткосрочный период вычисляется по формуле \(\pi (q) = q \cdot ( p - v) - f \). Компания продает свою продукцию по цене \(p = 400 руб.\) за штуку, затраты на производство одной единицы продукции составляют \(v = 300 руб.\) за штуку, постоянные расходы предприятия \(f = 800 000 руб.\) в месяц. Определите наименьший месячный объем производства \(q\) (шт.), при котором прибыль предприятия будет не меньше \(700 000 руб.\) в месяц.
Подробнее Узнать ответ КомментироватьВопрос B11 #1539 Математика (профиль)
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле \(A(\omega )=\frac{A_{0}\omega _{p}^{2}}{\left | \omega _{p}^{2}-\omega ^{2} \right |}\), где \(\omega\) – частота вынуждающей силы (в \(c^{-1}\)), \(A_0\) – постоянный параметр, \(\omega_{p}= 300 c^{-1}\) – резонансная частота. Найдите максимальную частоту \(\omega\), меньшую резонансной, для которой амплитуда колебаний превосходит величину \(A_0\) не более чем на 80%. Ответ выразите в \(c^{-1}\).
Подробнее Узнать ответ КомментироватьВопрос B11 #1553 Математика (профиль)
При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону \(l=l_{0}\sqrt{1-\frac{v^2}{c^2}}\) , где \(l_{0}=5м\) – длина покоящейся ракеты, \(c=3\cdot 10^5 км/с\) – скорость света, а \(v\) – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы её наблюдаемая длина стала не более \(4 м\)? Ответ выразите в км/с.
Подробнее Узнать ответ КомментироватьВопрос B11 #1567 Математика (профиль)
Емкость высоковольтного конденсатора в телевизоре \(C=4\cdot 10^{-6} Ф\). Параллельно с конденсатором подключен резистор с сопротивлением \(R= 4 \cdot 10^6 Ом\). Во время работы телевизора напряжение на конденсаторе \(U_0=54 кВ\). После выключения телевизора напряжение на конденсаторе убывает до значения \(U (кВ)\) за время, определяемое выражением \(t=\alpha R C log_{3} \frac{U_{0}}{U} (с)\), где \(\alpha=0,9\) – некоторая константа. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее \(28,8 с\). Ответ дайте в киловольтах.
Подробнее Узнать ответ КомментироватьВопрос B11 #1581 Математика (профиль)
Расстояние (в километрах) от наблюдателя, находящегося на высоте \(h\) километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле \(l = \sqrt{2Rh}\) , где \(R = 6400 км\) – радиус Земли. С какой высоты горизонт виден на расстоянии \(16\) километров? Ответ выразите в километрах.
Подробнее Узнать ответ КомментироватьВопрос B11 #1595 Математика (профиль)
Первые 270 км автомобиль ехал по шоссе со скоростью 72 км/ч, следующие 150 км - со скоростью 75 км/ч, а затем 66 км проехал за 1 час. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #1609 Математика (профиль)
При вращении ведёрка с водой на верёвке в вертикальной плоскости вода не выливается из него, если сила её давления на дно ведёрка неотрицательна во всех точках траектории. В верхней точке траектории сила давления воды на дно минимальна и равна \(P=m \left ( \frac{v^{2}}{L}-g \right )H\), где \(m\) – масса воды в кг, \(v\) – скорость движения ведёрка в м/с, \(L\) – длина веревки в метрах, \(g = 10 м/с^{2}\) – ускорение свободного падения. С какой минимальной скоростью \(v\) надо вращать ведёрко, чтобы вода не выливалась из него, если длина веревки равна 57,4 см? Ответ дайте в м/с.
Подробнее Узнать ответ КомментироватьВопрос B11 #1623 Математика (профиль)
Рейтинг \(R\) интернет-магазина вычисляется по формуле \(R=r_{пок}- \frac{r_{пок}-r_{экс}}{(k+1) \cdot \frac{0,02K}{r_{пок}+0,1}}\) , где \(r_{пок}\) - средняя оценка магазина покупателями (от 0 до 1), \(r_{экс}\) – оценка магазина экспертами (от 0 до 0,7) и К – число покупателей, оценивших магазин. Найдите рейтинг интернет‐магазина, если число покупателей, оставивших отзыв о магазине, равно 24, их средняя оценка равна 0,7, а оценка экспертов равна 0,4.
Подробнее Узнать ответ КомментироватьВопрос B11 #1637 Математика (профиль)
Скорость автомобиля v, разгоняющегося с места старта по прямолинейному отрезку пути длиной \(l\) км с постоянным ускорением \(a км/ч^{2}\), вычисляется по формуле \(v^{2}=2la\). Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 400 метров от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 8000 \(км/ч^{2}\). Ответ выразите в \(км/ч\).
Подробнее Узнать ответ КомментироватьВопрос B11 #1651 Математика (профиль)
Перед отправкой тепловоз издал гудок с частотой \(f_{0} = 490\) Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из‐за эффекта Доплера частота второго гудка \(f\) больше первого: она зависит от скорости тепловоза по закону \(f(v)=\frac{f_{0}}{1-\frac{v}{c}}\) (Гц), где \(c\) – скорость звука в воздухе (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы. Считать \(с\) = 340 м/с. Ответ выразите в м/с.
Подробнее Узнать ответ КомментироватьВопрос B11 #1665 Математика (профиль)
Кинетическая энергия тела, имеющего массу \(m\) (кг) и скорость \(v\) (м/с) равна \(E=\frac{mv^{2}}{2}\) (Дж). Какую наименьшую начальную скорость должна иметь пуля массой \(10\) грамм, чтобы при прохождении через неподвижную мишень передать ей энергию не меньше \(2400\) Дж, уменьшив при этом свою скорость не более, чем в два раза? (Считать, что в процессе полёта пули потери энергии не происходит). Ответ дайте в м/с.
Подробнее Узнать ответ КомментироватьВопрос B11 #1679 Математика (профиль)
Бетонная плита объемом \(2 м^{3}\) погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде? (Плотность бетона равна \(2000 кг/м^{3}\), плотность воды \(1000 кг/м^{3}\), считать \(g=9,8 Н/кг\)). Ответ дайте в килоньютонах.
Подробнее Узнать ответ КомментироватьВопрос B11 #2152 Математика (профиль)
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула \(F = 1,8 \cdot C + 32\), где \(C\) - градусы Цельсия, \(F\) - градусы Фаренгейта. Какая температура по шкале Цельсия соответствует \(176^{\circ}\) по шкале Фаренгейта?
Подробнее Узнать ответ КомментироватьВопрос B11 #2166 Математика (профиль)
Мальчик массой 45 кг стоит на лыжах. Длина каждой лыжи 1,5 м, ширина 10 см. Какое давление оказывает мальчик на снег? Ответ дайте в кПа. (Считать g=9,8 Н/кг).
Подробнее Узнать ответ КомментироватьВопрос B11 #2180 Математика (профиль)
При адиабатическом процессе для идеального газа выполняется закон \(pV^{k} = const\) , где \(p\) - давление в газе в паскалях, \(V\) – объем газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него \(k=\frac{5}{3}\) ) из начального состояния, в котором \(const=10^{5} Па·м^{5}\) , газ начинают сжимать. Какой наибольший объем \(V\) может занимать газ при давлениях \(p\) не ниже \(3,2\cdot 10^{6} Па\)? Ответ выразите в \(м^3\).
Подробнее Узнать ответ КомментироватьВопрос B11 #2194 Математика (профиль)
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \(F_{A}= \alpha \rho gr^{3}\), где \(\alpha = 4,2\) – постоянная, \(r\) – радиус аппарата в метрах, \(\rho = 1000 кг/м^{3}\) – плотность воды, а \(g\) – ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем \(336000 H\)? Ответ выразите в метрах.
Подробнее Узнать ответ КомментироватьВопрос B11 #2208 Математика (профиль)
Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой \(y=ax^{2}+bx\), где \(a=- \frac{1}{100} м^{-1}, b=1\) - постоянные параметры, \(x (м)\) - смещение камня по
горизонтали, \(y (м)\) - высота камня над землей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой \(8 м\) нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
Подробнее Узнать ответ КомментироватьВопрос B11 #2222 Математика (профиль)
Максимальная высота подъёма тела, брошенного под углом к горизонту, вычисляется по формуле \(h=\frac{(v \cdot sin \alpha)^{2}}{2g}\) , где \(v (м/c)\) - начальная скорость тела, \(\alpha\) - угол, под которым тело брошено к горизонту, \(g\) – ускорение свободного падения (считать, что \(g=10 м/с^2\)). С какой скоростью необходимо бросить мяч под углом \(30^{\circ}\) к горизонту, чтобы он поднялся на высоту \(5\) м?
Подробнее Узнать ответ КомментироватьВопрос B11 #2236 Математика (профиль)
Опорные башмаки шагающего экскаватора, имеющего массу \( m = 1260\) тонн представляют собой две пустотелые балки длиной \(l = 18\) метров и шириной \(s\) метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой \(p=\frac{mg}{2ls}\) , где \(m\) - масса экскаватора (в тоннах), \(l\) - длина балок в метрах, \(s\) - ширина балок в метрах, \(g\) - ускорение свободного падения (считайте \(g =10 м/с^2\)). Определите наименьшую возможную ширину опорных балок, если известно, что давление \(p\) не должно превышать \(140\) кПа. Ответ выразите в метрах.
Подробнее Узнать ответ КомментироватьВопрос B11 #2250 Математика (профиль) <- Есть решение
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Подробнее Узнать ответ КомментироватьВопрос B11 #2269 Математика (профиль) <- Есть решение
Имеется два сосуда. Первый содержит 30 кг, а второй -20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится во втором сосуде?
Подробнее Узнать ответ КомментироватьВопрос B11 #2284 Математика (профиль) <- Есть решение
Товарный поезд движется со скоростью 35 км/ч. По соседним путям его обгоняет электричка, идущая со скоростью 95 км/ч. Длина товарного поезда равна 780 м. Найдите длину электрички (в метрах), если известно, что мимо товарного поезда она прошла за 54 секунды.
Подробнее Узнать ответ КомментироватьВопрос B11 #2303 Математика (профиль) <- Есть решение
Катер и плот одновременно отплыли вниз по реке. Пройдя 16 км, катер развернулся и пошел вверх по реке. Пройдя 12 км, он встретился с плотом. Какова собственная скорость катера, если скорость течения реки 4 км/ч? Ответ выразите в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2322 Математика (профиль) <- Есть решение
Из пункта F круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 15 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2341 Математика (профиль) <- Есть решение
Пловец потерял под мостом флягу, но заметил это только через 3 мин. Повернув назад, он догнал флягу в 100 м от моста. Найдите скорость течения реки. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2560 Математика (профиль) <- Есть решение
Расстояние между городами \(A\) и \(B\) равно \(131\) км. Из города \(A\) в город \(B\) выехал автомобиль, а через 19 минут 10 секунд следом за ним со скоростью \(\frac {308}{3}\) км/ч выехал мотоциклист, догнал автомобиль в городе \(C\) и повернул обратно. Когда он вернулся в \(A\), автомобиль прибыл в \(B\). Найдите расстояние от \(A\) до \(C\). Ответ дайте в километрах.
Подробнее Узнать ответ КомментироватьВопрос B11 #2577 Математика (профиль) <- Есть решение
Первую четверть трассы автомобиль ехал со скоростью 60 км/ч, вторую четверть – со скоростью 120 км/ч, третью четверть – со скоростью 110 км/ч, а последнюю – со скоростью 132 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2598 Математика (профиль) <- Есть решение
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 18250 рублей, через три года был продан за 13304,25 рублей.
Подробнее Узнать ответ КомментироватьВопрос B11 #2731 Математика (профиль) <- Есть решение
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 134%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 2%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Подробнее Узнать ответ КомментироватьВопрос B11 #2750 Математика (профиль) <- Есть решение
Первый велосипедист выехал из поселка по шоссе со скоростью 17 км/ч. Через час после него со скоростью 13 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа 10 минут после этого догнал первого. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2765 Математика (профиль) <- Есть решение
Фермер в октябре продавал картофель в два раза дешевле, чем в марте. При этом выручка от продажи картофеля в октябре оказалась на 53% ниже по сравнению с мартом. Определите, на сколько процентов меньше картофеля продал фермер в октябре, чем в марте?
Подробнее Узнать ответ КомментироватьВопрос B11 #2788 Математика (профиль) <- Есть решение
Рабочие прокладывают туннель длиной 1,2 км, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 15 дней.
Подробнее Узнать ответ КомментироватьВопрос B11 #2807 Математика (профиль) <- Есть решение
Имеется 10 ящиков. В некоторых из них лежат по 10 ящиков меньшего размера, а в некоторых из меньших ящиков лежат еще по 10 ящиков. Сколько всего ящиков, если заполненных оказалось 54? (Заполненным считается ящик, в котором находится хотя бы один ящик меньшего размера).
Подробнее Узнать ответ КомментироватьВопрос B11 #2826 Математика (профиль) <- Есть решение
Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2845 Математика (профиль) <- Есть решение
На изготовление 112 деталей первый токарь затрачивает на 2 часа меньше, чем второй токарь на изготовление 150 таких же деталей. Известно, что первый токарь за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй токарь?
Подробнее Узнать ответ КомментироватьВопрос B11 #2864 Математика (профиль) <- Есть решение
Три числа составляют арифметическую прогрессию. Если первые два оставить, а к третьему прибавить сумму двух первых, то полученные числа составят геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
Подробнее Узнать ответ КомментироватьВопрос B11 #2883 Математика (профиль) <- Есть решение
Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2902 Математика (профиль) <- Есть решение
Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?
Подробнее Узнать ответ КомментироватьВопрос B11 #2921 Математика (профиль) <- Есть решение
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 12 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2940 Математика (профиль) <- Есть решение
Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2959 Математика (профиль) <- Есть решение
Теплоход проходит по течению реки от пункта А до пункта В, расстояние между которыми 120 км, и после стоянки возвращается в пункт А. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 2 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 30 часов после отплытия из него. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #2990 Математика (профиль) <- Есть решение
Три каменщика разной квалификации выложили кирпичную стену, причем первый работал 6 ч, второй – 4 ч, а третий – 7 ч. Если бы первый каменщик работал 4 ч, второй – 2 ч и третий – 5 ч, то было бы выполнено 2/3 всей работы. За сколько часов каменщики закончили бы кладку, если бы они работали все вместе одно и то же время?
Подробнее Узнать ответ КомментироватьВопрос B11 #3117 Математика (профиль) <- Есть решение
Бригаде грузчиков поручили перевезти 120 контейнеров. После перевозки 36 контейнеров автомобиль заменили более мощным, грузоподъемность которого на 10 контейнеров больше. В результате общее число рейсов по сравнению с первоначально планируемым сократилось вдвое. Сколько контейнеров перевозила за один рейс первая машина?
Подробнее Узнать ответ КомментироватьВопрос B11 #3236 Математика (профиль) <- Есть решение
Моторная лодка проплыла против течения реки 150 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше, чем на путь против течения. Найдите скорость течения реки, если скорость лодки в неподвижной воде равна 20 км/ч. Ответ дайте в км/ч.
Подробнее Узнать ответ КомментироватьВопрос B11 #3255 Математика (профиль) <- Есть решение
Два экскаватора, работая совместно, могут вырыть котлован за 48 ч. Если первый проработает 40 ч, а второй – 30 ч, то будет выполнено 75% всей работы. За какое время может вырыть котлован второй экскаватор, работая отдельно?
Подробнее Узнать ответ КомментироватьВопрос B11 #3316 Математика (профиль) <- Есть решение
Куплен товар двух сортов: первого на 4500 руб. и второго на 2100 руб. Второго
сорта куплено на 2 кг меньше первого и стоит он на 200 рублей дешевле. Сколько
килограммов товара первого сорта куплено? (Если решений несколько, то в ответ написать наибольшее)
Подробнее Узнать ответ КомментироватьВопрос B11 #3398 Математика (профиль) <- Есть решение
Василий ведет машину со скоростью 40 км/ч. Он хочет проезжать каждый километр на 1 минуту быстрее. На сколько ему надо увеличить скорость? (Ответ дать в км/ч)
Подробнее Узнать ответ КомментироватьВопрос B11 #3417 Математика (профиль) <- Есть решение
Ученик читал книгу 4 дня. Число страниц, прочитанных им в первые три дня, относится как \(\frac{1}{5};\frac{1}{3};\frac{1}{10}\). В четвертый день он прочитал 15% от числа страниц, прочитанных во второй день. Сколько всего страниц прочитано, если известно, что число страниц, прочитанных во второй день, больше числа всех страниц, прочитанных в другие дни, на 8 страниц.
Подробнее Узнать ответ КомментироватьВопрос B11 #3646 Математика (профиль) <- Есть решение
Разность между седьмым и утроенным четвертым членами целочисленной арифметической прогрессии равна 7, а произведение второго и пятого членов равно -20. Найдите сумму всех положительных трехзначных членов прогрессии.
Подробнее Узнать ответ КомментироватьВопрос B11 #3665 Математика (профиль) <- Есть решение
Концентрация полезного вещества в растворе 60%. Масса раствора 3 кг. Сколько чистой воды надо добавить, чтобы концентрация полезного вещества уменьшилась до 20%?
Подробнее Узнать ответ КомментироватьВопрос B11 #3789 Математика (профиль) <- Есть решение
Найдите двузначное натуральное число, если известно, что разность между самим числом и утроенной суммой его цифр равна 7, а при делении произведения цифр на их сумму в частном получается 2 и в остатке 1.
Подробнее Узнать ответ КомментироватьВопрос B11 #3808 Математика (профиль) <- Есть решение
Одна акция компании "А", три акции компании "В" и пять акций компании "С" вместе стоят 100 тысяч рублей. Две акции компании "А", четыре акции компании "В" и три акции компании "С" вместе стоят 150 тысяч рублей. Какова общая стоимость (в тыс. руб) семи акций компании "А", семнадцати акций компании "В" и двадцати одной акции компании "С"
Подробнее Узнать ответ КомментироватьВопрос B11 #3827 Математика (профиль) <- Есть решение
Барсик съедает миску корма за 40 секунд, а Мурка такую же миску корма съедает за 1 минуту. Утром к миске с кормом подошел Барсик и начал есть, а через 10 секунд к этой же миске прибежала Мурка и стала помогать Барсику. Спустя 10 секунд после этого Мурка прогнала Барсика и продолжила доедать корм одна. Определите, за какое время была съедена миска корма? Ответ дайте в секундах.
Подробнее Узнать ответ Комментировать